PRADIS
УЧЕБНОЕ ПОСОБИЕ
ПРОГРАММНЫЙ КОМПЛЕКС ДЛЯ АВТОМАТИЗАЦИИ МОДЕЛИРОВАНИЯ НЕСТАЦИОНАРНЫХ ПРОЦЕССОВ В МЕХАНИЧЕСКИХ СИСТЕМАХ И СИСТЕМАХ ИНОЙ ФИЗИЧЕСКОЙ ПРИРОДЫ
ВЕРСИЯ 4.2
Содержание
1.1. ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ПРОЦЕССОВ В ИНЖЕНЕРНЫХ РАСЧЕТАХ
1.2. АВТОМАТИЗАЦИЯ ФОРМИРОВАНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ТЕХНИЧЕСКОГО ОБЪЕКТА
1.3. ВЫЧИСЛИТЕЛЬНЫЙ АЛГОРИТМ КОМПЛЕКСА PRADIS
2.1. ПРОЦЕДУРА ОБСЛУЖИВАНИЯ СИСТЕМНОГО КАТАЛОГА
2.2. ПРОЦЕДУРА ВЫПОЛНЕНИЯ ЗАДАНИЯ
3. ФОРМИРОВАНИЕ И ЗАПУСК ПРОСТЕЙШЕГО ЗАДАНИЯ
3.1. ПОДГОТОВКА ТЕКСТА ЗАДАНИЯ
3.2. РАСЧЕТ КОЛЕБАНИЙ ПРУЖИННОГО МАЯТНИКА. ПЕРВЫЕ ОШИБКИ И ПЕРВЫЕ РЕЗУЛЬТАТЫ
3.3. ЗАПУСК ЗАДАНИЯ ДЛЯ УЖЕ СФОРМИРОВАННОЙ МОДЕЛИ
4. ВЫВОД И ОТОБРАЖЕНИE РЕЗУЛЬТАТОВ
4.1. ОРГАНИЗАЦИЯ ВЫВОДА РЕЗУЛЬТАТОВ В КОМПЛЕКСЕ PRADIS
4.2. НЕКОТОРЫЕ ПРОГРАММЫ РАСЧЕТА ВЫХОДНЫХ ПЕРЕМЕННЫХ
4.3. ПРОГРАММЫ ОТОБРАЖЕНИЯ РЕЗУЛЬТАТОВ РАСЧЕТОВ
4.3.1. Оперативное отображение выходных переменных в ходе расчета
4.3.2. Программы символьного отображения результатов расчета
4.3.3. Отображение результатов расчета в виде графиков на экране дисплея.
4.4. ПРОГРАММА РАСЧЕТА КОЛЕБАНИЙ МАЯТНИКА, ИСПОЛЬЗУЮЩАЯ БОЛЬШЕ ВОЗМОЖНОСТЕЙ ВЫВОДА ИНФОРМАЦИИ
5. АНАЛИЗ БОЛЕЕ СЛОЖНОЙ ЗАДАЧИ
5.1. РАЗДЕЛ ОПИСАНИЯ ДАННЫХ И СРЕДСТВО ЗАМЕНЫ ПАРАМЕТРОВ
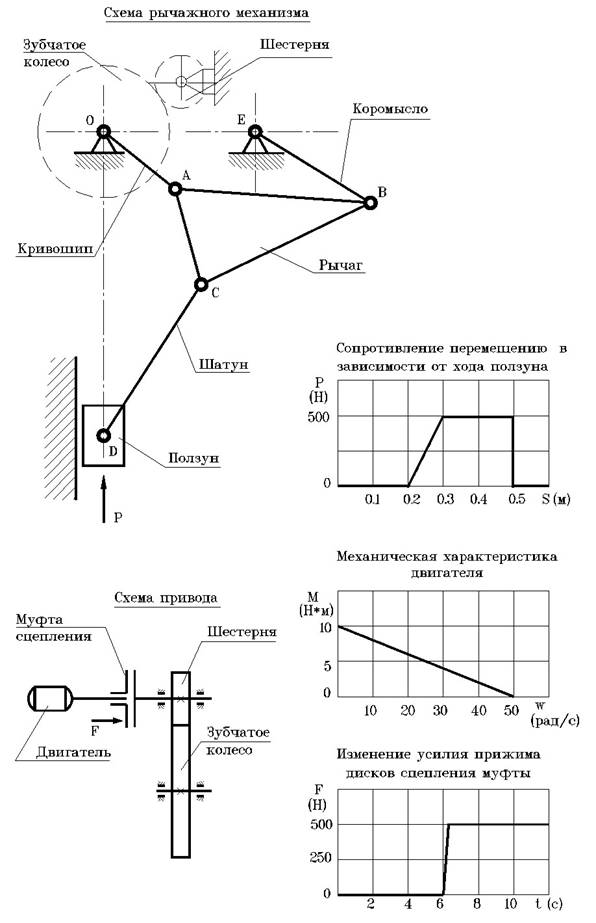
5.2. ОПИСАНИЕ БОЛЕЕ СЛОЖНОЙ ЗАДАЧИ (МОДЕЛИРОВАНИЕ ТЕХНОЛОГИЧЕСКОЙ МАШИНЫ)
5.3. ФОРМИРОВАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ТЕХНОЛОГИЧЕСКОЙ МАШИНЫ.
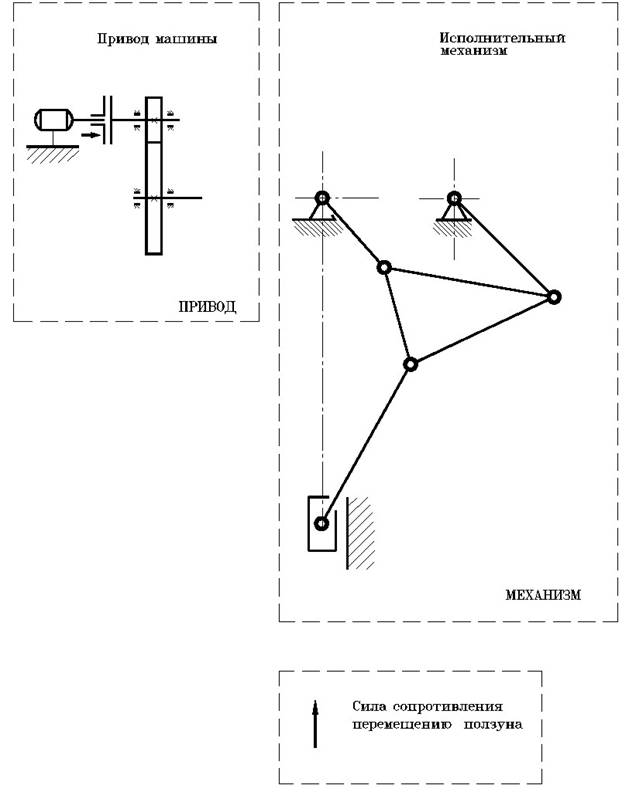
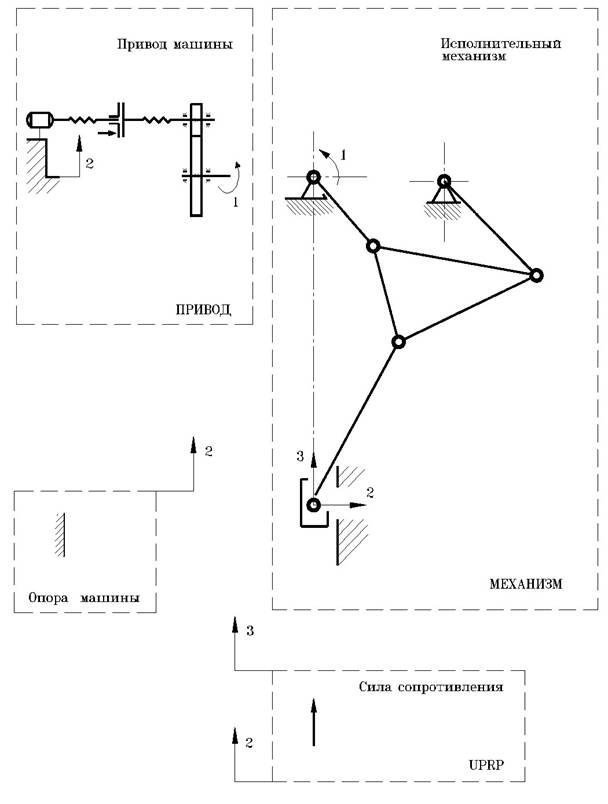
5.3.3. Модель исполнительного механизма.
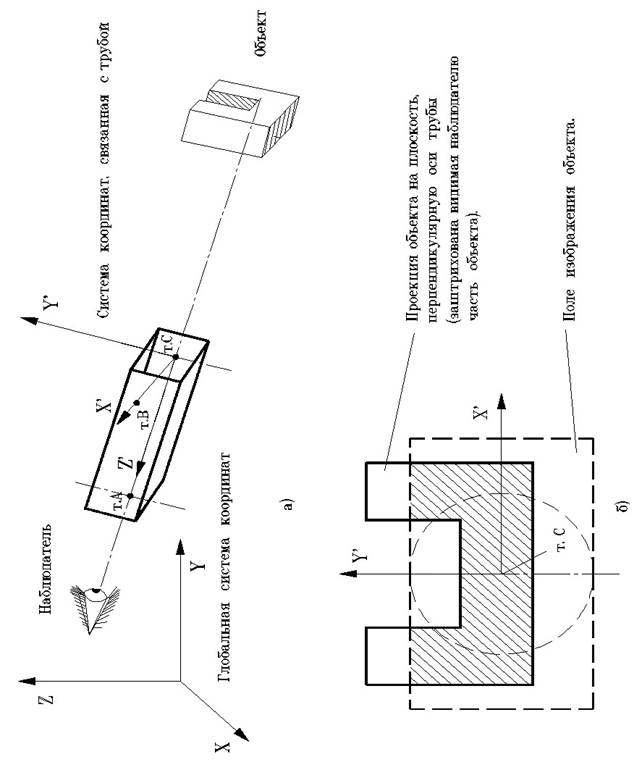
5.3.4. Изображение объекта – раздел SHOW.
5.3.5. Сборка модели технологической машины из отлаженных фрагментов.
5.3.6. Использование инструкции препроцессора $INCLUDE.
6. ДОПОЛНИТЕЛЬНЫЕ ВОЗМОЖНОСТИ УПРАВЛЕНИЯ РАБОЧЕЙ ПРОГРАММОЙ
6.1. ИЗОБРАЖЕНИЕ ИСПОЛНИТЕЛЬНОГО МЕХАНИЗМА
6.1.1. Управление составом и цветом изображения для слоя
6.1.2. Использование нестандартных графических образов
6.1.3. Связь слоя изображения с подвижной системой координат
6.2. УПРАВЛЕНИЕ ТОЧНОСТЬЮ РЕШЕНИЯ СИСТЕМЫ ДУ
6.2.1. Окончательный текст программы, реализующей модель механизма
6.2.2. Ключевые параметры, определяющие локальную погрешность интегрирования
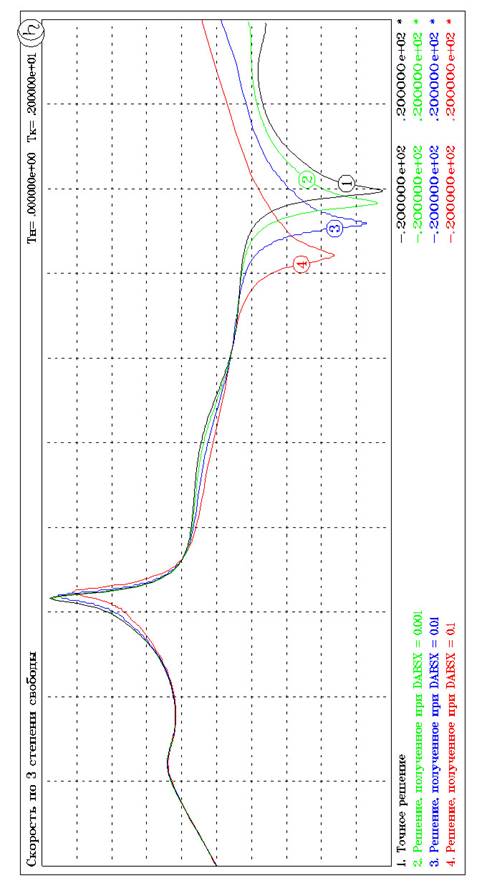
6.2.3. Численные эксперименты с локальной погрешностью..
6.3. РАСЧЕТ ТЕХНОЛОГИЧЕСКОЙ МАШИНЫ
АННОТАЦИЯ
Этот документ рассчитан на пользователя, приступающего к изучению программного комплекса PRADIS. Наряду с изложением первичной информации, необходимой начинающему, разбирается решение нескольких задач. Авторы стремились к изложению материала от простого к сложному. Как и для всех подобных пособий, крайне необходимо, чтобы все действия, описанные здесь, выполнялись параллельно на ЭВМ. Желательно, чтобы не только воспроизводились действия авторов, но и выполнялись задания, приведенные в тексте. Это поможет Вам быстрее начать самостоятельно использовать комплекс для решения своих задач.
Краткая аннотация глав настоящего документа.
Во ВВЕДЕНИИ коротко рассмотрены алгоритмы, положенные в основу комплекса PRADIS. Дается общее представление о методе формирования математической модели объекта в виде системы дифференциальных уравнений. Показана последовательность численных методов, позволяющая анализировать математическую модель объекта на заданном интервале времени.
ВТОРАЯ ГЛАВА рассказывает о процедурном обеспечении программного комплекса. Рассмотрены процедуры обслуживания системного каталога и выполнения задания, доступные пользователю в стандартной конфигурации комплекса.
В ТРЕТЬЕЙ ГЛАВЕ на примере математической модели пружинного маятника показана последовательность действий, необходимых для формирования и анализа математической модели с помощью комплекса PRADIS. Рассмотрены простейшие средства отображения результатов расчета.
В ЧЕТВЕРТОЙ ГЛАВЕ более подробно рассмотрены средства отображения результатов. Разбирается несколько новых программ расчета выходных переменных и программ отображения. Вводится понятие указателя на внутреннюю переменную.
В начале ПЯТОЙ ГЛАВЫ рассказывается о средствах замены параметров и восстановления состояния расчета, актуальных для больших задач. Далее рассмотрен более сложный пример – формирование математической модели технологической машины для проектного анализа. На примере расчета одного из фрагментов машины разбирается ключевой параметр программы интегрирования, отвечающий за максимальный шаг интегрирования. Вводятся средства изображения объекта в ходе расчета.
В ШЕСТОЙ ГЛАВЕ разбираются вопросы формирования более сложного изображения объекта и другие возможности, предоставляемые пользователю разделом $SHOW. Рассмотрены ключевые параметры программы интегрирования, отвечающие за точность решения системы дифференциальных уравнений.
1. ВВЕДЕНИЕ
Создавая это пособие, авторы несколько раз приступали к написанию ведения. Это оказалось неожиданно сложной задачей, хотя о чем писать было более или менее ясно. Даже когда уже была вчерне написана пятая глава, введение по-прежнему оставалось "темным пятном на светлом фоне концессионных работ". Изложение вводных соображений по поводу применения при проектировании математических моделей через два-три абзаца неизбежно скатывалось к глубокому теоретизированию. В зависимости от настроения писавшего, текст мог быть наполнен фиолетовой философской меланхолией или слоноподобными математическими формулами. Результат, однако, всегда получался одинаковым. Во-первых, он всегда нравился автору. Во-вторых, никто посторонний прочитать его не мог, что служило надежным замком к документу в целом.
Нам кажется, что облегченная форма и стиль, который для документов подобного назначения можно отнести к фривольным, все же помогли нам решить эти проблемы. Однако, насколько это соответствует действительности – решать читателю.
1.1. ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ПРОЦЕССОВ В ИНЖЕНЕРНЫХ РАСЧЕТАХ
В начале главы хотелось бы предложить вниманию читателя
СКАЗКУ О ТОМ, КАК ИНЖЕНЕР ВАСЯ ДЕЛАЛ
ЛЕБЕДКУ, И ЧТО ИЗ ЭТОГО ВЫШЛО
для студентов младшего возраста и
инженеров-стажеров
В некотором царстве, некотором государстве существовала фабрика. И работали на этой фабрике инженер Вася и рабочий Ваня. Если говорить точнее, работало там великое множество народу, но остальные люди в нашем повествовании играют роль несущественную, малозаметную.
Сказали как-то БОЛЬШИЕ ЛЮДИ Ивану поднять некий груз на высоту 1 метр 10 сантиметров и погрузить его на платформу транспортную. Однако, как ни старался, как ни бился над грузом бедолага, так и не смог его даже на 10 сантиметров приподнять. Тогда пошел Ваня к инженеру и говорит:
- Слышал я, что в странах заморских, зарубежья неближнего, для подъема тяжелых грузов используют сильномогучие лебедки. Помоги мне, выручи из беды. Научи, как сделать лебедку.
Научил Вася Ваню, и тот сделал лебедку. Однако, только стал поднимать он на платформу груз, как канат у лебедки оборвался, и груз ударил Ваню по ноге. Больно-пребольно. Пошел Ваня к Васе и сказал:
- Вася, ты неправ!
Вася и сам видел, что он неправ. Поэтому он достал шибкомудрую книжку "Сопротивление материалов" и стал считать канат лебедки на прочность от нагрузки детерминированной и линейной. Скоро сказка сказывается, да не скоро дело делается. День считал Вася канат, два считал, сто листов бумаги писчей извел, две ручки шариковых до основания исписал. На третий день посчитал все Василий. Сделали они для лебедки новый канат. Стал Иван поднимать груз во второй раз, но тут подул ветер, груз стал раскачиваться, и блок лебедки, на котором был накручен канат, обломался. Но на этот раз не от статической нагрузки, а от нагрузки динамической. И ударил груз Ивана по руке. Больно-пребольно. И в третий раз пошел Ваня к Васе и сказал ему:
- Вася, ты неправ!
Вася понял, что и на этот раз он неправ. Достал он тогда жуткокрутую книжку "Детали машин" и стал учитывать всякие динамические нагрузки, действующие на блок и канат стохастически и нелинейно. День учитывал, два учитывал, на третий, наконец, все нагрузки учел. Сделали они лебедке новый блок. Накрутили на него канат. Стал Иван поднимать груз на платформу, но на этот раз не выдержал двигатель асинхронный, с фазным ротором. Задымился, загорелся двигатель от нагрузки неимоверной. И упал груз Ивану на голову. Не потому, что двигатель сгорел от перегрузки. Это бы еще ничего. А потому, что тормоз у лебедки был нормально разомкнутым, а не нормально замкнутым. Ничего не сказал на этот раз Ваня Васе – увезли его на карете скорой в палаты белые, реанимационные.
Вася снова понял, что он неправ. Но книжку нужную не успел уже достать, потому что пришли за ним люди казенные, и повели его под руки белые в карету под названьем "воронок". И не видел никто с тех пор ни Васи, ни лебедки Васиной. И называлось с тех пор дело последнее "лебедкиной песнею".
А Иван-дурак вылечился и поехал в края дальние, столицы белокаменные. Выучился он там на инженера. И то ли умнее он стал, после того как груз упал ему на голову, то ли выучили его там хорошо, но стал он проектировать такие лебедки, что ни в сказке сказать, ни пером описать. А канаты он считал, и блоки, исходя не только из статической, но и динамической нагрузки. А двигатели асинхронные подбирал не только по моменту номинальному, но считал и токи среднеквадратичные, и баланс тепловой. А тормоза у него были только нормально замкнутые, с запасом большим.
И я там был, и лебедками его пользовался. Мед-пиво на платформы грузовые грузил, себя и друзей ими потчевал. Да вот беда – по усам текло, а в рот не попало.
Конечно, сказка – ложь, да в ней намек, добрым молодцам урок:
1. Как правило, проектирование нового технического объекта должно сопровождаться грамотным инженерным расчетом.
2. При расчете необходимо учитывать большое количество факторов. Это – различные процессы (механические, электрические, тепловые), которые происходят в объекте, и их взаимное влияние.
Один из методов, который позволяет учитывать при расчете большое количество факторов – это математическое моделирование. В ходе моделирования процессы в объекте или его элементах описываются в виде системы дифференциальных уравнений. Таким образом, удается на модели воспроизвести поведение объекта, взаимодействие тех или иных его элементов в какой-то конкретной ситуации. Например, если бы Вася использовал при проектировании математическое моделирование, то груз все три раза падал бы не на реального Ваню, а на его модель. Кроме того, в ходе моделирования он легко смог бы определить нагрузки на канат, блок и двигатель. Авария двигателя в модели могла бы подсказать ему (если уж он не читал Правила Госгортехнадзора), что тормоз должен быть нормально замкнутым.
Перечисленные преимущества предварительного анализа проектируемого объекта на математической модели очевидны. Конечно, некоторых трудностей можно было бы избежать и обычным расчетом. Скорее всего, канат не оборвался бы, тормоз сработал бы и т.д. Но учесть некоторые вещи при обычном расчете было бы достаточно сложно. Например, раскачивание груза приведет к динамическим нагрузкам на канат и блок, неравномерность нагрузок на блок приведет к неравномерности крутящего момента на двигателе и неизвестно, как эта неравномерность скажется на тепловом режиме двигателя. Невозможность учета многих факторов в таких расчетах приводит к большим и часто неоправданным коэффициентам запаса. А самым парадоксальным оказывается то, что даже эти большие коэффициенты запаса иногда оказываются недостаточными.
Но с другой стороны, получить математическую модель объекта в виде системы дифференциальных уравнений тоже не так просто. Кто пробовал этот хлеб, тот подтвердит, что это сложно даже при ограниченном количестве степеней свободы в модели. Во-первых, нужно для заданных параметров объекта рассчитать коэффициенты уравнений. Во-вторых, при заданной структуре объекта не ошибиться в записи самих уравнений. Эти два пункта оказываются, как правило, ключевыми и весьма сложными. Скорость создания моделей "вручную" мала, так как очень высока вероятность ошибок на этом пути, а обнаружение и поиск этих ошибок – нетривиальная задача. В-третьих, нужно решить полученную систему уравнений. В последние два десятилетия в этом направлении накоплен уже значительный опыт применения ЭВМ, поэтому эта задача носит более технический характер и, как нам кажется, относительно более проста. Однако, вся проблема в комплексе весьма внушительна, и для инженера применение этой технологии является, как правило, непозволительной роскошью. Во всяком случае, никто не позволит тратить каждый раз один-два-три месяца, год, два и т.д. на создание разовых математических моделей конкретных объектов.
Единственная возможность применения математического моделирования в инженерной практике – каким-то образом сократить время на формирование математической модели (системы дифференциальных уравнений) и весь процесс от формирования до анализа автоматизировать. В следующем подразделе в общих чертах описано, как реализована автоматизация формирования модели в комплексе PRADIS.
1.2. АВТОМАТИЗАЦИЯ ФОРМИРОВАНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ТЕХНИЧЕСКОГО ОБЪЕКТА
Когда мы говорим об автоматизации формирования математической модели в виде системы дифференциальных уравнений, мы, конечно, не имеем в виду некоторые распространенные в настоящее время подходы. Так, для многих современных программ нужно ввести полученную пользователем систему уравнений. Эта система должна быть предварительно записана пользователем, исходя из его знаний предметной области. Другие программные средства предлагают пользователю рассчитать и ввести коэффициенты для системы уравнений заранее заданного вида. Многие программы таких типов не требуют, чтобы дифференциальные уравнения были разрешены относительно старшей производной и допускают, что система дифференциальных уравнений может быть дополнена нелинейными алгебраическими и трансцендентными уравнениями. Все это хорошо, но уравнения должен записать все-таки сам пользователь. "Как аргонавты в старину", мы садимся за стол и выписываем уравнения Лагранжа второго рода, страдая над каждым интегралом, загоняя непокорные диаметры, длины и модули упругости в коэффициенты уравнения и безбожно ошибаясь в знаках. А потом месяцами отлаживаем модель.
В PRADIS формирование математической модели в виде системы дифференциальных уравнений, как и ее последующий анализ, осуществляется автоматически. Для формирования системы уравнений используется узловой метод.
Входом для программного комплекса является описание моделируемого объекта на языке описания объекта, содержащее такую информацию:
1) информация о структуре объекта (топология объекта);
2) параметры объекта (описание геометрии, материалов и т.д.);
3) описание рассчитываемых выходных переменных, которые непосредственно необходимы пользователю в результате решения задачи анализа.
Как видно из приведенного здесь списка, нет необходимости вводить какую-либо информацию о коэффициентах уравнений и об их структуре. Каким же образом программа все-таки получает необходимую систему уравнений?
Представим себе некий детский конструктор, в котором из кубиков можно сделать различные объекты – дома, машины – модели вещей, существующих в реальном мире. Для построения каждой конкретной модели нужно взять определенный набор кубиков соответствующего вида и соединить их тоже определенным образом. Понятно, что для модели дома нужно взять другие кубики и соединить их по-другому, чем для модели башенного крана. Однако, модели домиков разных размеров, но одной структуры, можно собрать из аналогичных по форме кубиков, различающихся только размером. Говорят, что модели дома и башенного крана имеют разную структуру (топологию), а две модели дома, различающиеся размерами – одинаковую.
Аналогично осуществляется формирование математической модели с использованием комплекса PRADIS. Для этого пользователю необходимо из существующего набора "кирпичиков" (моделей элементов) выбрать нужные для построения требуемой модели объекта. Базовый набор моделей элементов в PRADIS отличается от набора "кирпичиков" в детском конструкторе в основном тем, что в конструкторе имеется ограниченное количество элементов одинакового вида. Например, 5 кубиков со стороной 10 см, 3 кубика со стороной 20 см, десять параллелепипедов определенного размера и т.д. В то же время, если уж какой-то элемент есть в библиотеке комплекса PRADIS, то количество элементов такого типа, которые можно использовать в модели объекта, не ограничено. Каждый из выбранных для формирования модели объекта "кирпичиков" может соединяться с другими кирпичиками в строго определенных местах (степенях свободы). Количество и назначение степеней свободы модели элемента определяется в ее описании. Выбирая различные способы соединения моделей элементов, можно описать объекты различной структуры.
|
|
|
|
Рис. 1.1. |
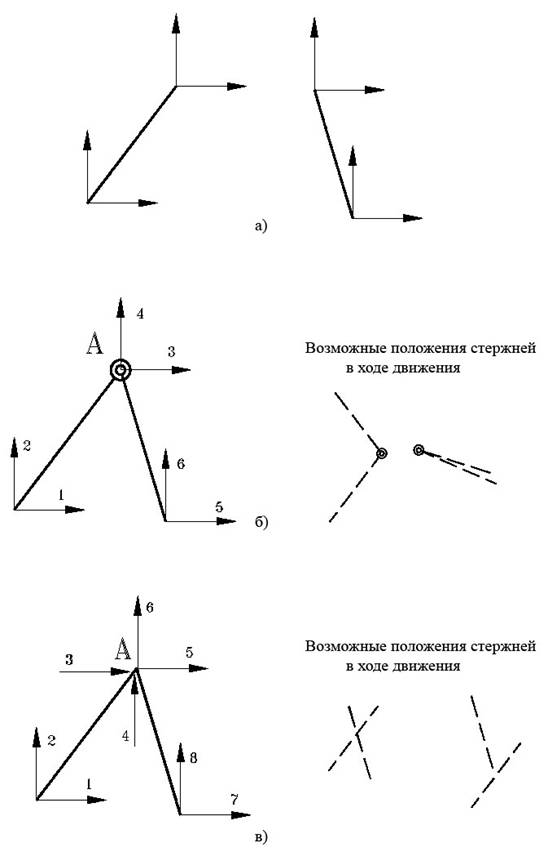
Иллюстрация формирования модели объекта из «кирпичиков»: а) в качестве «кирпичиков» выбраны два стержня, каждый из которых имеет четыре степени свободы; б) шарнирное соединение стержней (две степени свободы общие); в) стержни не имеют общих степеней свободы. |
Допустим, пользователь хочет описать объект, состоящий из двух шарнирно скрепленных стержней. Если стержни податливые, то каждый из стержней имеет четыре степени свободы (рис. 1.1а). Совмещая стержни в точке A и объявляя, что концы стержней в этой точке движутся одинаково (имеют одни и те же степени свободы), получим шарнирное соединение стержней. При этом, каждый из стержней по-прежнему описывается четырьмя степенями свободы, но их номера для одного из концов каждого стержня совпадают (рис. 1.1б). В то же время, совмещая стержни в точке A, но продолжая каждый из стержней описывать четырьмя степенями свободы с разными номерами, получим два стержня, совершающих независимое движение (рис. 1.1в).
С математической точки зрения, соединение нескольких элементов по какой-то степени свободы аналогично записи для этой степени свободы уравнения равновесия. При этом нужно выписать такие уравнения для всех степеней свободы системы, в том числе и для степени свободы (степеней свободы), связанной с системой координат, относительно которой рассматривается движение. В PRADIS степень свободы, связанная с системой координат, называется базовой. Описание структуры полной системы уравнений равновесия фактически эквивалентно описанию структуры объекта, поэтому такие уравнения часто называются топологическими. Состояние объекта в каждой из степеней свободы описывается независимой переменной, которая подлежит определению в ходе анализа. Значения независимых переменных в каждой из степеней свободы, с которыми соединяется модель элемента, связаны уравнениями, характеризующими данный элемент (или компоненту). Поэтому такие уравнения называются компонентными. Подстановка компонентных уравнений в уравнения равновесия приводит к автоматическому формированию системы дифференциальных уравнений – математической модели объекта. В общем случае это – система нелинейных дифференциальных уравнений, которая в дальнейшем должна решаться численным методом.
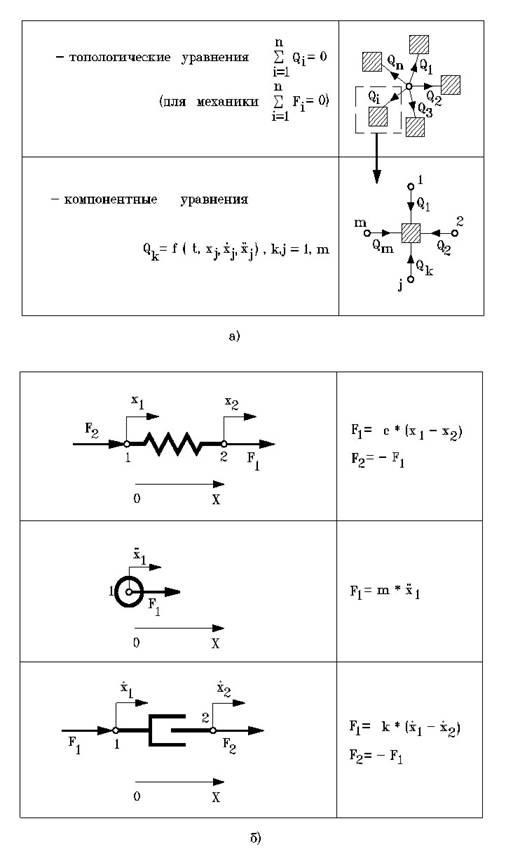
Описанный алгоритм формирования математической модели соответствует узловому методу, основные положения которого иллюстрирует рис.1.2. На том же рисунке приводятся компонентные уравнения для простейших элементов механических систем – одномерного упругого, одномерного вязкого и точечного инерционного элементов.
Если внимательно рассмотреть алгоритм формирования математической модели системы по узловому методу, можно прийти к нескольким заключениям:
1) Процесс формирования математической модели узловым методом является универсальным постольку, поскольку универсальны уравнения равновесия. Его можно применять в тех областях физики, где такие уравнения существуют и имеют физический смысл, т.е. практически повсеместно (механика – уравнения равновесия, электроника – первый закон Кирхгофа, термодинамика – уравнение баланса тепловых потоков, гидравлика – баланс массовых расходов и т.д.).
2) Разнообразие задач, которые можно решать с использованием этого подхода, ограничено разнообразием имеющихся в распоряжении инженера "кирпичиков" – моделей элементов.
|
|
|
|
Рис. 1.2. |
Узловой метод формирования математической модели: а) общая схема метода; б) примеры компонентных уравнений для простейших элементов. |
Состав библиотеки моделей элементов является основным фактором, накладывающим ограничения на универсальность PRADIS. Однако, нужно отметить, что в настоящее время базовая библиотека моделей элементов насчитывает несколько десятков разновидностей "кирпичиков", и их количество постоянно возрастает. И еще. Здесь можно продолжить аналогию с детским конструктором. Хороший столяр всегда может сделать новые кирпичики и, соответственно, расширить возможности по сборке моделей разных объектов. Так же и здесь. Инженер, владеющий предметной областью и знающий программирование, может воспользоваться штатными процедурами комплекса PRADIS для расширения базовой библиотеки моделей элементов.
1.3. ВЫЧИСЛИТЕЛЬНЫЙ АЛГОРИТМ КОМПЛЕКСА PRADIS
Итак, получена математическая модель объекта в виде системы дифференциальных уравнений. Следующим этапом анализа является интегрирование этой системы уравнений. Естественно, что этот процесс осуществляется численно с использованием ЭВМ. В этом документе у нас нет возможности в деталях разобрать алгоритм вычислительного ядра комплекса. Однако, некоторая информация все-таки нужна, так как очень трудно пользоваться любым инструментом, не представляя принципов, на которых он основан. Поэтому здесь в общих чертах рассматривается алгоритм интегрирования, к которому, по мере необходимости, мы будем возвращаться в последующих главах. Пользователи, которым для работы с комплексом понадобится более подробное знакомство с основными используемыми математическими методами, должны обратиться к соответствующей документации "Программный комплекс для автоматизации моделирования нестационарных процессов в механических системах и системах иной физической природы. Основные математические методы".
Сформированная система дифференциальных уравнений решается на заданном временном интервале. Этот интервал делится на несколько отрезков ("шаги интегрирования"). Величина шага интегрирования не является постоянной и зависит от большого количества факторов: насколько анализируемый процесс является спокойным, какие требования точности заданы пользователем, каковы ограничения на шаг интегрирования. Задаваясь величиной шага интегрирования и используя формулы интегрирования типа известных из школьного курса физики
S(i) = S(i-1) + V(i-1) · dt + A(i) · dt2 /2
V(i) = V(i-1) + A(i) · dt,
можно перейти от системы дифференциальных уравнений к системе нелинейных алгебраических и трансцендентных уравнений. На самом деле все не так просто – в решаемой системе дифференциальных уравнений могут присутствовать производные не только по времени, но и по пространственным координатам. Однако, это не меняет существа дела. Для них тоже можно применить аппроксимации типа конечно-разностных или конечно-элементных. Разница заключается лишь в том, что за дискретизацию пространства в комплексе отвечает не программа интегрирования, а модели элементов. Полученная на шаге интегрирования система нелинейных уравнений (СнЛУ) решается итерационно методом Ньютона. На каждой итерации метода Ньютона для нахождения очередного приближения к решению формируется и решается система линейных алгебраических уравнений (СЛАУ). Для решения СЛАУ используется метод Гаусса. Общая схема алгоритма программы интегрирования комплекса PRADIS приводится на рис.1.3.
|
|
|
|
Рис 1.3. |
Алгоритм работы программы интегрирования комплекса PRADIS |
Исходя из сказанного выше, шаг интегрирования может быть неудачным по нескольким причинам:
1) был выбран слишком большой шаг интегрирования, и полученное для следующего шага решение не удовлетворяет заданной точности;
2) был выбран слишком большой шаг интегрирования, и не удается с заданной точностью за максимально разрешенное число итераций получить решение системы нелинейных уравнений;
3) из-за ошибки описания структуры объекта не удается решить систему линейных алгебраических уравнений.
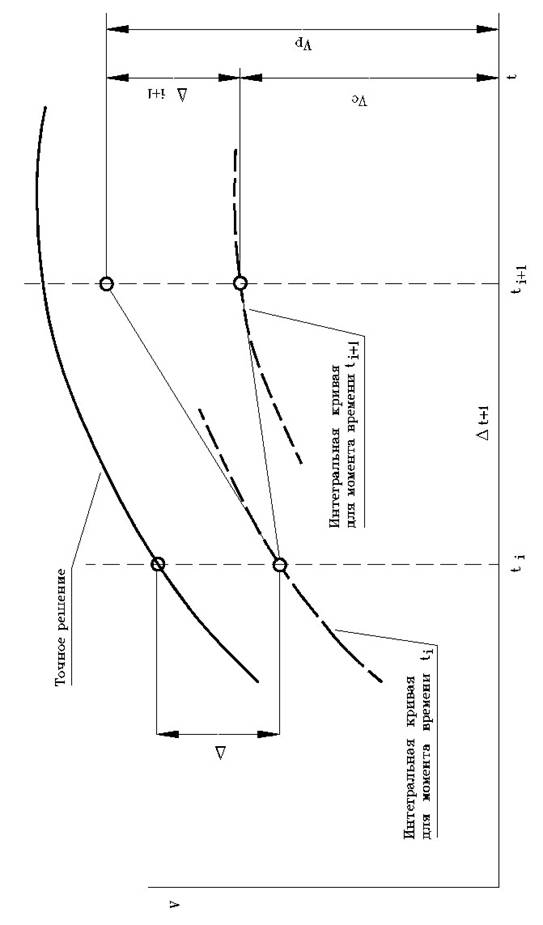
В третьем случае происходит безусловное завершение вычислений, и здесь уже пользователь должен поработать над описанием структуры объекта. В первом и втором случаях комплекс пытается удовлетворить требованиям точности и уменьшить шаг интегрирования. Тогда неудавшийся шаг интегрирования фиксируется как потерянный по величине локальной погрешности (1), или как потерянный по несходимости решения системы нелинейных уравнений (2). Нужно сказать, что серьезность перечисленных выше причин, по которым шаг интегрирования признается неудачным, увеличивается сверху вниз. Так, несходимость решения системы нелинейных уравнений приводит к большему количеству неприятных последствий для пользователя, чем потеря шага по локальной погрешности, а неудача решения системы линейных алгебраических уравнений – более серьезная неприятность, чем потеря шага по несходимости системы нелинейных уравнений.
Пользователь может управлять работой программы интегрирования, задавая конкретные значения тех или иных ключевых параметров. Можно менять точность решения системы дифференциальных уравнений, точность решения системы нелинейных алгебраических уравнений, количество допускаемых итераций на шаг интегрирования и т.д. Однако, для этого требуется определенный расчетный опыт. Поэтому при рассмотрении с помощью PRADIS простейших задач рекомендуется воспользоваться параметрами программы интегрирования, задаваемыми по умолчанию. В дальнейшем, как это и рекомендовано в пособии, можно вносить в свой арсенал несколько новых возможностей по управлению процессом интегрирования, начиная с самых простейших. После того, как Вы почувствуете, как и на что влияет тот или иной параметр, можно переходить к изучению и использованию других возможностей по управлению работой программы интегрирования.
1.4. КАК ЧИТАТЬ ЭТО ПОСОБИЕ
Настоящий документ не является полным, исчерпывающим и формальным описанием программного комплекса PRADIS. Основное его назначение – дать пользователю некоторую информацию для совершения нескольких первых, самых трудных шагов в освоении расчетов с использованием комплекса.
Один из ведущих отечественных методологов ("методолухов", как он сам любил повторять, говоря о себе и своих учениках) рассказал такую байку. Изучая методы и средства обучения, некий зарубежный педагог совершал поездку по фермам Дикого Запада. Тамошние ковбои, как известно, славятся искусством бросать лассо. И там путешественник стал свидетелем процесса обучения этому делу молодого необстрелянного ковбоя. Старый волк своего дела очень долго и, видимо, достаточно эмоционально что-то рассказывал молодому человеку. После этого абитуриенту дали в руки лассо, и он с большим знанием дела и отменной точностью стал арканить нужных животных. В чем заключался секрет этого метода обучения, история до нас не донесла. Авторы осознают, что достижение старого ковбоя в педагогическом плане является некоторым недостижимым эталоном. По крайней мере, обучить работе с комплексом PRADIS только посредством теоретической беседы, пусть и длительной, они не берутся. В этом смысле они готовы даже признать, что бросание лассо является занятием более теоретическим, чем проведение сложных инженерных расчетов. В последнем случае крайне важен настойчивый тренинг и обратная связь с практикой – тесный контакт инженера-расчетчика с конструктором или доводчиком реального объекта. Поэтому с первых шагов использования комплекса PRADIS, как и другого подобного программного обеспечения, необходимо стремиться как можно больше считать.
Отсюда вытекает основная идея изложения – продемонстрировать приемы работы с программным комплексом, решая с пользователем несколько более или менее простых задач. Авторы сделали все возможное, чтобы пользователь смог изучать это пособие во время своих поездок в метро, за письменным столом или вместо детектива, перед отходом ко сну. Однако, нас давит груз сомнений, что сделанного оказалось не достаточным и без компьютера не обойтись. Поэтому основным приемом изучения предлагаемого здесь материала является повторение за компьютером всех предлагаемых в этом пособии задач и внимательный анализ получаемых результатов. Предварительно неплохо было бы бегло просмотреть описание языка комплекса PRADIS, а в дальнейшем постоянно обращаться к тем главам этого документа, в которых говорится о тех или иных синтаксических конструкциях входного языка комплекса.
В некоторых местах авторы намеренно воспроизводят нештатные ситуации, которые могут быть вызваны как типичными ошибками пользователя, так и незнанием некоторых особенностей вычислительного алгоритма комплекса или неучетом особенностей решаемой задачи. Это вызвано двумя причинами.
Во-первых, создается более непринужденная атмосфера общения. Пользователю кажется, что и авторы этого пособия могут ошибаться, и это должно привести к невольному улучшению настроения и поднятию авторитета пользователя в собственных глазах (особенно, если ошибка или причина нештатной ситуации была замечена до того, как в ней признались авторы). На самом деле, настоящие ошибки авторов заметны далеко не всем, в том числе и самим авторам. Именно поэтому такие ошибки, уже в силу того, что они не заметны широкому кругу пользователей и узкому кругу разработчиков ("ниньзя", так сказать), должны носить жуткий и разрушительный характер. Авторы будут благодарны любому бдительному пользователю, обнаружившему вражеского агента, затесавшегося в наших рядах.
Во-вторых, большое количество типовых приемов работы с программным обеспечением типа комплекса PRADIS связано как раз с преодолением такого рода ситуаций. Изучение этих приемов, как нам кажется, не может ухудшить квалификацию расчетчика. В дальнейшем, приобретая расчетный опыт (а, возможно, и опыт разработчика программного обеспечения), пользователь может сам расширить этот арсенал.
После изучения этого пособия (возможно, изучения только некоторой его части), пользователь, вооруженный знаниями методики моделирования и овладевший арсеналом приемов работы в затруднительных ситуациях, должен перейти к самостоятельной работе с комплексом. В этой работе ему помогут другие документы по программному комплексу PRADIS, в первую очередь справочные пособия. Не думаем, что в самостоятельном полете его ожидает безоблачное существование, но искренне и горячо этого ему желаем. Будем рады, если у него время от времени будут появляться потребность или желание вернуться к некоторым избранным главам этого пособия – для уточнения ответа на какой-либо тонкий вопрос, восстановления в памяти последовательности действий в том или ином случае или просто без определенной цели – побродить мысленно по знакомым местам. В этом случае авторы будут считать свою задачу выполненной.
1.5. РЕЗЮМЕ
Таким образом, введение содержало сведения в основном пропагандистского характера. Суть их можно свести к нескольким пунктам:
1. Во избежание несчастных случаев считайте, считайте и считайте.
2. Есть расчеты и расчеты. К инженерным расчетам высшей категории предлагают отнести расчеты на основе подробной математической модели, отражающей взаимосвязь всех существенных процессов в анализируемом объекте.
3. Критикуются попытки моделирования, когда модель анализируемого объекта из уравнений Лагранжа второго рода формируется "вручную", поскольку этот хлеб несколько зачерствел.
4. Для ускорения процесса п.2 можно использовать методы автоматизации моделирования, которые авторы, очень кстати к этому разговору, реализовали в рамках комплекса PRADIS.
5. Если пользователь все-таки решил воспользоваться рекомендациями авторов, то далее нужно его несколько припугнуть, что, дескать, процесс является все равно не простым, и если что не получится, то сам виноват.
6. Авторы полагают, что пользователь, вообще говоря, человек свободный, и ему больше нечего делать, как только приступить не просто к прочтению настоящего руководства, но и к его изучению сидя за компьютером.
7. В целом, авторы подходят к рядовому пользователю дружественно, и местами выражают надежду, что ему не только удастся оседлать программу интегрирования, но и стать неплохим столяром, смастерив пару-тройку моделей элементов, отсутствовавших в библиотеке моделей элементов.
2. ПРОЦЕДУРЫ КОМПЛЕКСА PRADIS
В полной конфигурации комплекса PRADIS имеется две процедуры, доступные пользователю: процедура выполнения задания SLANG и процедура обслуживания системного каталога ARM (в случае, если в вашей версии комплекса доступен каталог SRV). Каждая из процедур комплекса при ее вызове без параметров выдает краткую справочную информацию о доступных режимах работы.
Немного более подробно изучим эти процедуры комплекса.
2.1. ПРОЦЕДУРА ОБСЛУЖИВАНИЯ СИСТЕМНОГО КАТАЛОГА
Для получения информации о доступных режимах набираем команду
> ARM
(Здесь и далее символом > обозначается промптер, т.е. приглашение операционной системы вашей ЭВМ на ввод информации)
Если все нормально, то в ответ на команду ARM на экране дисплея получаем следующее сообщение:
====================================================================
Использование: arm [<ключ> <имя1> [<имя2> [имя3 ... [имяN] ] ] ]
Процедура обработки бинарного каталога PRADIS.
<ключ>
? выводит справку по компонентам, содержащимся в
бинарном каталоге
+ включает компоненты в бинарный каталог и строит
динамические плагин-библиотеки, если возможно.
Если не задано <имя1...N>, то пытается подключить
шаблоны
из файла templet.txt в текущем каталоге.
p автоматически строит динамические плагин
библиотеки и включает компоненты в бинарный каталог.
u добавляет функции в пользовательскую библиотеку
user.lib.
# просто строит динамические плагин-библиотеки, если
возможно
! включает компоненты в бинарный каталог
Если не задано <имя1...N>, то пытается подключить
шаблоны
из файла templet.txt в текущем каталоге.
- исключает компоненты из бинарного каталога
* выводит содержимое встроенной помощи
<имя1...N> не применимо к этому ключу
n создаёт пустой бинарный каталог в текущей директории
<имя1...N> не применимо к этому ключу
<имя1...N>
имена запрашиваемых компонентов
====================================================================
Из этой краткой справки можно заключить, что назначение процедуры обслуживания системного каталога следующее:
· получение краткой информации о текущем составе библиотек комплекса;
· получение более подробной оперативной справочной информации о различных компонентах комплекса;
· добавление модулей в библиотеки комплекса и их исключение из состава библиотек комплекса.
Нужно отметить, что справочная информация, предоставляемая процедурой обслуживания системного каталога, является менее полной, чем информация, содержащаяся в справочниках по системе. Ее основное назначение – освежить в памяти те или иные особенности конкретной компоненты комплекса, с которой пользователь знакомился по документации. Если в вашей версии комплекса процедура обслуживания системного каталога отсутствует, то всю справочную информацию, требующуюся в этом пособии, следует брать из соответствующих справочников.
Для получения краткой информации о текущем составе комплекса можно воспользоваться командами с ключами ? и *. По команде
> ARM ?
на экране дисплея появляется краткая информация о всех включенных в состав комплекса модулях – моделях элементов, программах расчета выходных переменных, программах реализации графических образов и программах отображения. Кроме вывода на экран информация всегда дублируется в текстовом файле SYSPRINT.TXT текущего каталога. Этот файл может быть обработан стандартными средствами операционной системы (например, текстовым редактором).
Приведем пример. Пользователю необходимо найти, как называется модель элемента, реализующего одномерный упругий хрупко разрушающийся элемент, и получить более подробную справочную информацию об этой модели. Получаем справку о всех включенных в системный каталог модулях. Фрагмент файла SYSPRINT.TXT, интересующий пользователя в этом случае, выглядит следующим образом:
И м я К р а т к о е н а з н а ч е н и е
...
BELTV Характеристика ремня, задаваемая таблично с учетом вытяжки
ремня
BLOK Упругий восьмиугольный элемент (кирпичик)
BRK Упругая связь с хрупким разрушением
...
Из полученной информации видно, что название интересующего нас элемента – BRK. Для получения более подробной информации по этой модели, введем команду
> ARM ? BRK
На экран и в файл SYSPRINT.TXT в этом случае будет выведена более подробная информация о модели элемента BRK.
Кроме получения информации по включенным в комплекс модулям имеется возможность получить оглавление встроенного HELP'a (названия всех возможных тем, по которым можно получить справочную информацию). По команде
> ARM *
в файл SYSPRINT.TXT выводится список тем встроенного HELP'а. Фрагмент этого списка выглядит следующим образом:
...
ATRC BAL3DJ BAL3DK BALKA BELT
BELTV BLOK BORDER BRK BUKA
C CIL3DC CMASS COS3E CYLDR
DEBUG DEFORM DELR DFIA DFIB
...
Как видно из этого списка, кроме перечисления всех модулей, включенных в состав PRADIS и имеющих дополнительную справочную информацию, имеется справочная информация и о некоторых других вопросах, например, информация о программе интегрирования SHTERM, информация о режиме DEBUG и т.д.
Дополнительную справочную информацию, например, о программе интегрирования, можно получить, введя команду
> ARM ? SHTERM
Кроме описанных функций имеются возможности расширения состава комплекса или исключения некоторых компонент из его состава. Эти возможности относятся к числу расширенных и описаны в соответствующей документации. В вашей конфигурации комплекса они могут отсутствовать.
2.2. ПРОЦЕДУРА ВЫПОЛНЕНИЯ ЗАДАНИЯ
Программный комплекс PRADIS предназначен для анализа динамики технических систем. Задачи такого рода могут приводить к вычислениям значительной продолжительности. Поэтому выполнение задания в комплексе PRADIS осуществляется в пакетном режиме с возможностями интерактивного контроля за ходом вычислений. Любое задание описывается на входном языке и далее запускается на выполнение с помощью процедуры SLANG.
Ознакомимся с этой процедурой более подробно. Для получения информации о допустимых режимах введем команду
> SLANG
На экране дисплея в ответ на эту команду получаем следующее сообщение:
====================================================================
Использование: slang [-m|-r] [-e|-s] [-pgoN] name1 [name2]
Запустите решатель PRADIS в режиме симуляции.
Параметры:
name1 файл задания
описание на языке PARDISland
name2 имя предворительной задачи
(когда работа повторяется с уже построенной моделью)
Опции:
-pgoN запись графической 3D информации в файл
(ПГО файл), N обозначает счётчик выводимых точек
(выводить каждую N-ую точку), если N не задано,
то N=1
-e использовать расширенный формат вывода на экран (по
умолчанию)
-s использовать короткий формат вывода на экран
-r оценивать частоту вывода
на экран в реальном времени (по умолчанию),
значение частоты дисплея берётся
из параметра PRTTIME решателя PRADIS (по умолчанию 30)
текущее время должно показываться при условии
текущее время-последнее показанное время>частота
-m оценивать частоту вывода
на экран в модельном времени,
значение частоты вывода на экран берётся,
из параметра PRTTIME решателя PRADIS (по умолчанию 30),
текущее время должно показываться при условии
текущее время-последнее показанное время>частота
====================================================================
Итак, процедуру выполнения задания можно использовать в двух режимах. Допустим, вы хотите выполнить анализ модели редуктора, текст которой записан на входном языке PRADIS и содержится в файле REDUCT. Запуск задания на выполнение в этом случае будет выглядеть следующим образом:
> SLANG REDUCT
В ходе выполнения задания осуществляется оперативное отображение части полученных данных на экране дисплея. Кроме того, в текущем каталоге сохраняются файлы, необходимые для дальнейшей работы с моделью и полученными результатами. Например, файл с расширением DAT содержит результаты расчета и в дальнейшем обрабатывается программой POSTPROCESSOR.
В любом случае в текущем каталоге всегда остается файл SYSPRINT.TXT, содержащий вывод и сообщения всех обрабатывающих программ, а также временную статистику для задания.
В дальнейшем Вам может понадобиться
· продолжить расчет с прерванного места
· выполнить новый расчет для сформированной на предыдущем этапе модели, заменив некоторые исходные данные
· изменить способ отображения полученных в ходе расчета результатов без повторения расчета.
Допустим, все необходимые вам действия описаны на входном языке PRADIS и содержатся в файле REDNEW. Запуск задания, содержащегося в REDNEW, для модели REDUCT будет выглядеть следующим образом:
> SLANG REDNEW REDUCT
2.3. РЕЗЮМЕ
Коротко повторим наши достижения в освоении комплекса PRADIS.
1. В комплексе PRADIS имеется две процедуры пользователя – ARM и SLANG.
2. Процедура ARM служит для получения оперативной справочной информации по компонентам комплекса и расширения состава его библиотек.
3. Процедура SLANG предназначена для выполнения задания.
4. Краткая информация о допустимых режимах работы процедур может быть получена вызовом процедур без параметров.
5. Все процедуры комплекса оставляют в текущем каталоге файл SYSPRINT.TXT, в котором содержится вывод и сообщения программ обработки.
3. ФОРМИРОВАНИЕ И ЗАПУСК ПРОСТЕЙШЕГО ЗАДАНИЯ
В качестве иллюстрации использования программного комплекса PRADIS рассмотрим задачу анализа колебаний одномерного пружинного маятника.
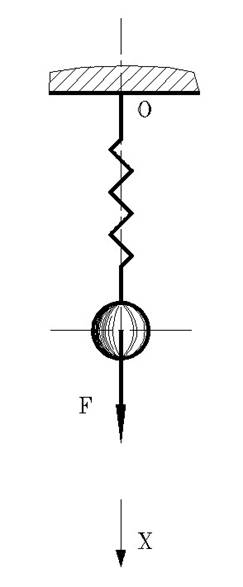
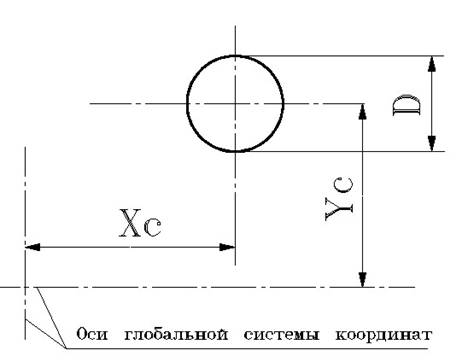
Постановка задачи. Определить скорость и перемещение с течением времени для одномерного пружинного маятника, состоящего из точечной массы 1 кг, подвешенной на пружине жесткостью 10 Н/м. Моделируется ситуация, когда груз поддерживается рукой и в начальный момент времени резко отпускается, так что сила тяжести груза (F) прикладывается к маятнику в начальный момент времени. Расчетная схема рассматриваемого объекта изображена на рис.3.1.
|
|
|
|
Рис. 3.1. |
Расчетная схема пружинного маятника. |
3.1. ПОДГОТОВКА ТЕКСТА ЗАДАНИЯ
Подготовка расчетной модели начинается с выбора глобальной системы координат (определение размерности физического пространства, в котором рассматривается движение объекта, выбор направления координатных осей). В нашем случае движение рассматривается в одном измерении. Начало координат (точка O) находится в месте закрепления пружины. За положительное направление координатной оси принято направление сверху вниз.
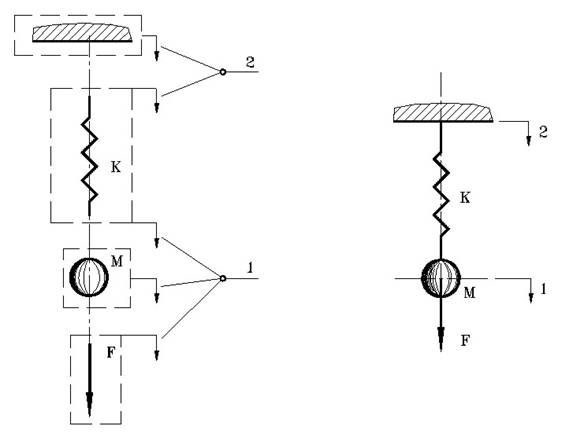
Вторым шагом в подготовке модели является декомпозиция системы на элементы, т.е. выделение элементов, из которых состоит исследуемый объект. Обычно, параллельно проводится работа по подбору для каждого элемента объекта соответствующей ему модели элемента. В нашем случае выделены следующие элементы и соответствующие им модели (см. также рис. 3.2):
- основание, служащее для закрепления пружины (система отсчета);
- осевой идеально упругий элемент с двумя степенями свободы (K, пружина);
- точечный инерционный элемент (M, масса);
- источник постоянной силы (F, сила тяжести).
|
|
|
|
Рис. 3.2. |
Модели элементов и нумерация степеней свободы для математической модели одномерного пружинного маятника. |
Естественно, что для описания структуры интересующего вас объекта предпочтительно использовать элементы, имеющиеся в составе библиотеки моделей. Поэтому при подборе моделей элементов, соответствующих элементам моделируемого объекта, используется справочная информация по библиотеке моделей элементов. Обычно это или справочник по библиотекам комплекса или справка, полученная по команде
> ARM ?
Иногда необходимый элемент может отсутствовать в библиотеке моделей элементов. Чаще всего, это характерно для случая, когда вы приступаете к решению первых нескольких задач из какой-либо новой предметной области. В этом случае тем или иным способом должна быть решена задача расширения базовой библиотеки моделей новыми элементами. Как правило, эта задача решается непосредственным пользователем штатными средствами комплекса, или обращаются за помощью в расширении библиотеки моделей элементов к разработчикам комплекса.
После того, как список необходимых элементов подобран, получают более подробную информацию по выбранным элементам, например, с помощью той же команды ARM. В нашем случае ее вызов выглядел так:
> ARM ? K M F
В этой справке важной является информация о количестве степеней свободы, которые имеет каждый из элементов. Так, при описании элемента K должно быть использовано две степени свободы, а при описании M и F – одна степень свободы. Говорят, что элемент K имеет две ветви (является двухполюсником), а элементы M и F – по одной ветви (однополюсники). Для описания моделируемого объекта необходимо ветви выбранных элементов соединить так, чтобы воспроизвести реальные связи этих элементов в моделируемом объекте.
Наконец, соединив выбранные элементы в соответствующих точках, получаем степени свободы (узлы) анализируемой системы. Полученные узлы нумеруем положительными целыми числами. При этом необходимо иметь в виду, что степень свободы, соответствующая перемещению основания, в данном случае закреплена.
На этом предварительный этап подготовки задачи закончен.
Воспользовавшись любым текстовым редактором, создадим файл c программой на входном языке PRADIS. Вспомним (см. описание языка), что описание моделируемой технической системы ("описание объекта") содержится в разделе FRAGMENT. Он может содержать подразделы, озаглавленные
· # BASE - описание закрепления фрагмента,
· # STRUCTURE - описание структуры фрагмента,
· # OUTPUT - описание вывода для фрагмента.
Описание закрепления и структуры пружинного маятника на языке PRADIS в нашем случае выглядит следующим образом:
# BASE : 2 { - закреплена 2-я степень свободы системы}
# STRUCT :
Пружина 'K (2,1; 10); Масса 'M (1; 1)
Сила тяжести 'F (1; 9,81)
В этом описании говорится, что объект имеет 2 узла и состоит из трех элементов. Для описания свойств элемента "Пружина" используется модель элемента K, элементу "Масса" соответствует модель элемента M, элементу "Сила тяжести" – модель элемента F. Закреплен 2-й узел, с ним связана первая ветвь элемента "Пружина". В 1-ом узле соединяются элементы "Пружина", "Масса" и "Сила тяжести". Рассматривая более подробно описание элемента, заметим, что оно состоит в общем случае из следующих частей:
- идентификатор элемента (каждый элемент снабжается уникальным идентификатором). Максимальная длина идентификатора – 32 символа (буквы, цифры, точки, пробелы, символы подчеркивания; на первом месте обязательно находится буква). В нашем примере идентификаторы – «Пружина», «Масса» и «Сила тяжести»;
- имя модели элемента. В нашем примере – это "K", "M" и "F";
- номера узлов, с которыми соединяется модель, разделитель (;), и список параметров модели.
Например, элемент «Пружина» соединен своей первой ветвью с узлом 2, второй ветвью – с узлом 1 объекта. В соответствии с описанием этого элемента, для него задается один параметр – величина жесткости. В нашем случае – 10 Н/м.
Информация, заключенная в фигурные скобки, является комментарием и транслятором игнорируется. Комментарии в PRADIS-программе, как и в программе на любом другом языке, можно использовать для улучшения читаемости текста программы, а также для сохранения информации, которая может понадобиться при дальнейшей работе. Однако нужно помнить, что вложенные комментарии не допускаются. При трансляции программы текст, содержащийся в комментариях, на экран дисплея и в файл SYSPRINT.TXT не попадает.
Другим важным элементом описания объекта является описание вывода для фрагмента. Весь вывод в комплексе PRADIS осуществляется путем вызова в подразделе OUTPUT соответствующих программ расчета выходных переменных. Более подробно вопрос выбора нужных ПРВП будет обсуждаться в следующей главе. Здесь скажем только, что в нашем случае для вывода перемещения и скорости точечного инерционного элемента (1-я степень свободы рассматриваемой системы) мы использовали, соответственно, программы расчета выходных переменных S и V:
# OUTPUT :
Перемещение 'S (1; 1.0); Скорость 'V (1; 1.0)
Вызовы программ расчета выходных переменных во многом похожи на описания элементов. В описание вызова входит
- идентификатор выходной переменной ("Перемещение", "Скорость");
- имя программы, используемой для расчета соответствующей выходной переменной ("S", "V");
- внутренние переменные и параметры, передаваемые в программу расчета выходных переменных. В нашем случае это номер узла (1) и, после разделителя, – единичный масштаб вывода.
Закончив описание объекта, приступим к описанию задания.
В общем случае задание состоит из двух основных разделов:
· RUN – описание задания на расчет переходных процессов в технической системе;
· PRINT – описание задания на отображение полученных результатов.
Управление работой всех программ, вызываемых в разделах задания RUN и PRINT, осуществляется с помощью ключевых параметров. Большинство этих параметров имеют значения по "умолчанию", и если пользователь согласен с принимаемым по умолчанию значением, то этот параметр при вызове программы просто не указывается. Ключевые параметры, определенные для каждой программы, и их значения по умолчанию приводятся в справочной информации по этим программам.
Для проведения расчета в разделе RUN вызывается программа интегрирования (в случае, если речь идет о расчете сложного процесса, можно вызвать несколько программ интегрирования). Для каждой из них может быть задано большое количество ключевых параметров, управляющих точностью решения, устанавливающих ограничения на шаг и даже модифицирующих схему интегрирования. Это позволяет настроить программу на конкретную задачу, что для средних и больших расчетов позволяет экономить много времени. Однако часто, особенно при решении таких простейших задач, как рассматриваемая, можно определить только интервал интегрирования, оставив все остальные параметры настройки программы интегрирования без изменения (приняв их по умолчанию). В этом простейшем случае мы решили рассмотреть движение маятника на протяжении интервала времени 1с от начала процесса. Расчет будем проводить методом Штермера, задав только интервал интегрирования (этот ключевой параметр является обязательным при описании вызова программы интегрирования):
$ RUN :
Расчет колебаний маятника'SHTERM (END=1)
В структуру описания вызова программы интегрирования (описание вызова программы отображения результатов полностью аналогично), входит
· идентификатор программы (в данном случае "Расчет колебаний маятника");
· имя программы интегрирования (SHTERM, NEWMARK) или программы отображения;
· если это необходимо, то значения ключевых параметров программы, которые при данном вызове будут отличаться от значений ключевых параметров, задаваемых по умолчанию (в нашем случае установлено значение ключевого параметра END, определяющего интервал интегрирования);
· необязательный список отображаемых переменных (здесь отсутствует).
Аналогично делается описание задания на отображение результатов расчета – в разделе PRINT вызывается одна или несколько программ отображения. Задание на отображение результатов будет выглядеть так:
$ PRINT :
Результаты расчета'DISP ()
Описание задачи на языке PRADIS в обязательном порядке должно содержать заголовок $ END (признак окончания задания).
3.2. РАСЧЕТ КОЛЕБАНИЙ ПРУЖИННОГО МАЯТНИКА. ПЕРВЫЕ ОШИБКИ И ПЕРВЫЕ РЕЗУЛЬТАТЫ
Записав полученную программу в файл TEST, можем далее выполнить анализ колебаний описанной системы с помощью команды
> SLANG TEST
Первым шагом анализа является трансляция вашего описания объекта. В ходе трансляции пронумерованные строки задания (номера строк генерируются транслятором) выводятся на экран. На экран выводятся также предупреждающие сообщения и сообщения об обнаруженных синтаксических ошибках. Как это принято для процедур комплекса PRADIS, вывод дублируется в файл SYSPRINT.TXT текущего каталога. В случае, если код серьезности обнаруженных ошибок превышает 4, последующие этапы анализа не выполняются. Файл SYSPRINT.TXT при первом запуске нашего задания выглядел следующим образом:
1
2 $ FRAGMENT
^
W (S 501) Встретился неименованный заголовок $FRAGMENT. Может быть
только последним в описании объекта.
3 # BASE : 2
4 # STRUCT :
5 Пружина 'K (2,1; 10); Масса 'M (1; 1)
6 Сила тяжести 'F (1; 9,81)
^
E (S 075) Количество параметров модели элемента не соответствует
паспорту.
7 # OUTPUT :
8 Перемещение 'S (1; 1.0); Скорость 'V (1; 1.0)
9 $ RUN :
10 Расчет колебаний маятника'SHTERM (END=1)
11 $ PRINT :
12 Результаты расчета'DISP ()
13 $ END
M (S 702) Обнаружены серьезные синтаксические ошибки, препятствующие
дальнейшему выполнению анализа.
Файл WORK.DAT не появился или запрещён для чтения:
Очевидно, что кроме ожидаемой распечатки пронумерованных строк программы, нами были получены сообщения об ошибках (есть серьезная ошибка) и некоторые другие сообщения обрабатывающих и управляющих программ. Если это возможно, то позиция строки исходного текста, в которой допущена или обнаружена ошибка, указывается стрелкой (^) над текстом сообщения. Естественно, что пользователь может не получить сообщений о серьезных ошибках, если будет действовать более внимательно, чем авторы. В этом случае ему не придется исправлять программу и запускать ее повторно. Он может сразу приступить к анализу результатов. Или, наоборот, пользователь может допустить большее количество ошибок и разбираться с ними подольше. Рассмотрим подробнее сообщения, полученные в ходе синтаксического анализа нашей программы.
Предупреждающее сообщение ("W" – это признак предупреждающего сообщения) с номером S 501 имеет код серьезности 0, и вызвано тем, что на входном языке комплекса PRADIS допустимо наличие только одного неименованного фрагмента. В случае, если будет описано более одного неименованного фрагмента, информация о всех этих фрагментах, кроме последнего, будет утеряна. Вообще говоря, в данном случае это сообщение может быть проигнорировано, но хороший стиль программирования на PRADIS предполагает, что все фрагменты программы будут поименованы. Итак, выяснилось, что лучше дать нашему единственному фрагменту имя, например, "маятник".
Сообщение об ошибке (E) с номером S 075 имеет код серьезности 8 и в данном случае явилось причиной прерывания задания после завершения синтаксического анализа текста. Ошибка заключается в том, что для модели элемента F предполагается задание одного параметра. В нашем же случае, ошибочно поставив вместо десятичной точки запятую, мы определили не один параметр 9.81 (сила тяжести, действующая на тело массой 1кг), а два параметра – 9 и 81.
Сообщение транслятора (M) с номером S 702 говорит о том, что максимальный код обнаруженной ошибки превышает 4, что ведет к завершению задания после выполнения синтаксического анализа.
В конце файла SYSPRINT.TXT при нормальном завершении задания всегда содержится сообщение процедуры с номером P 001, содержащее данные о продолжительности различных этапов задания.
Внеся в программу указанные выше изменения, осуществим повторный запуск задания TEST на расчет. На этот раз авторам удалось избежать ошибок, и между синтаксическим анализом и получением файла SYSPRINT.TXT прошел более длительный промежуток времени, на протяжении которого выполнялись другие этапы задания (символьная факторизация, генерация рабочей программы, трансляция сгенерированной программы и сборка выполняемой программы анализа, выполнение полученной программы анализа, отображение полученных результатов). Перечень этих этапов, в зависимости от конфигурации и настройки вашего комплекса, может быть другим (например, могут отсутствовать этапы генерации рабочей программы, трансляции и редактирования связей). В ходе выполнения этих этапов на экране может отображаться информация и выдаваться сообщения, не требующие от пользователя каких-либо действий. Более подробно каждый из этапов и информация, которую может получить пользователь, будет обсуждена позже. Здесь рассмотрим полученные в ходе выполнения результаты. Файл SYSPRINT.TXT в нашем случае выглядел так:
1
2 $ FRAGMENT : маятник
3 # BASE : 2
4 # STRUCT :
5 Пружина 'K (2,1; 10); Масса 'M (1; 1)
6 Сила тяжести 'F (1; 9.81)
7 # OUTPUT :
8 Перемещение 'S (1; 1.0); Скорость 'V (1; 1.0)
9 $ RUN :
10 Расчет колебаний маятника'SHTERM (END=1)
11 $ PRINT :
12 Результаты расчета'DISP ()
13 $ END
M (S 700) Синтаксических ошибок не обнаружено.
M (P 004):(TURBOF:-1)
СООБЩЕНИЯ ПРОГРАММЫ ФАКТОРИЗАЦИИ.
Статистика результатов символьной факторизации:
Размерность системы уравнений: 2.
M (P 005):(TURBOF:-1)
Общее количество ненулевых элементов: 4.
Вторичных ненулевых элементов: 0.
Заполнение якобиана(%): 100.00
M (P 006):(TURBOF:-1)
Ненулевых элементов после главной диагонали (параметр Q): 0.50
Затраты на решение системы уравнений:
миллионов операций с плавающей точкой - 0.00
M (P 007):(TURBOF:-1)
миллионов инструкций процессора (целочисленные операции, переходы и присваивания) - 0.00
размер индексного массива (Кб) - 0.00
M (P 008):(TURBOF:-1)
Размеры сформированных векторов:
массив состояния расчета (Кб) - 0.625
адресный массив (Кб) - 0.320
M (P 043):(MESSAG:-1)
СООБЩЕНИЯ ПРОГРАММЫ ИНТЕГРИРОВАНИЯ.
Идентификатор программы: Расчет колебаний маятника
M (P 044):(MESSAG:-1)
Время начала интегрирования: 0.0000
Время окончания интегрирования: 1.0000
Размерность системы уравнений: 2.
Количество успешных шагов по времени: 104.
M (P 045):(MESSAG:-1)
Количество неудавшихся шагов по времени из-за:
- недопустимо большой локальной погрешности: 0.
- отсутствия сходимости процесса решения СнЛУ: 0.
M (P 046):(MESSAG:-1)
- неудовлетворительных результатов расчета в моделях элементов: 0.
- плохой обусловленности якобиана на шаге решения: 0.
M (P 047):(MESSAG:-1)
Общее количество успешных итераций: 177.
Общее количество потерянных итераций из-за:
- недопустимо большой локальной погрешности: 0.
M (P 048):(MESSAG:-1)
- отсутствия сходимости процесса решения СнЛУ: 0.
- неудовлетворительных результатов расчета в моделях элементов: 0.
M (P 049):(MESSAG:-1)
- плохой обусловленности якобиана на шаге решения: 0.
M (P 050):(MESSAG:-1)
СПИСОК ВЫХОДНЫХ ПЕРЕМЕННЫХ
N п/п Идентификатор Количество
компонентов
1. Скорость 1
2. Перемещение 1
3.3. ЗАПУСК ЗАДАНИЯ ДЛЯ УЖЕ СФОРМИРОВАННОЙ МОДЕЛИ
Обсуждавшиеся в конце предыдущего подраздела изменения можно внести непосредственно в файл TEST и повторить формирование и расчет модели с помощью команды
> SLANG TEST
Однако, все эти изменения коснулись только той части программы, которая относится к описанию задания. Поэтому можно внести изменения в задание на расчет без повторного формирования модели. Для этого, используя текстовый редактор, создадим текст нового задания на расчет:
$ RUN:
Расчет колебаний маятника'SHTERM (END=2;
Перемещение=(0,2),Скорость=(-5,5))
$ PRINT :
Результаты расчета'DISP (OUT=0.04; Перемещение=(0,2),
Скорость=(-5,5))
$ END
Поместим этот текст в файл с именем T и выполним повторное задание для сформированной модели TEST:
> SLANG T TEST
На этот раз в SYSPRINT.TXT (и на экране) после заголовка $ RUN появилось следующее сообщение:
W (S 515) В программе отсутствует заголовок $RESTORE.
Расчет будет проводиться с нулевого момента
времени.
Причиной этого сообщения явилось то обстоятельство, что мы не захотели продолжить предыдущий расчет (с момента времени 1 с). Поэтому, интегрирование будет проведено с нулевого момента времени, а результаты предыдущего расчета уничтожены, о чем и предупреждает программа.
В остальном получены те же результаты, что и предполагалось: графики отображаемых переменных по ходу расчета выводились в заданных масштабах и на этот раз были похожи на синусоиды, был рассчитан один полный период (и даже немного больше) колебаний маятника.
Если пользователю хочется продолжить расчет с места его прерывания, нужно применить заголовок $RESTORE. Например, текст задания для расчета второго периода колебаний нашего маятника с использованием уже полученных ранее результатов расчета, выглядит так:
$ RESTORE :
$ RUN :
Расчет колебаний маятника'
SHTERM (END=4; Перемещение=(0,2),Скорость=(-5,5))
$ PRINT :
Результаты расчета'DISP (OUT=0.08;Перемещение=(0,2),
Скорость=(-5,5))
$ END
В этом случае расчет начнется с момента времени 2 с после начала процесса. Результаты будут отображаться для всего рассчитанного интервала времени (от начала процесса до 4 с). С учетом этого шаг вывода для программы отображения увеличен еще в два раза.
И последнее замечание. В приведенном примере расчета мы задали возможные интервалы изменения переменных, пользуясь уже полученными в ходе предварительного расчета результатами. Однако, для первого расчета выполнение этого требования может оказаться затруднительным. Поэтому на практике обычно поступают так. Для первого расчета выбираются такие возможные интервалы изменения переменных, которые гарантированно обеспечат отображение переменных на всем протяжении расчета или за пределами которых значение отображаемой переменной пользователя не интересует. В ходе последующих расчетов эти интервалы могут уточняться. Если проводится только один расчет и в определении интервалов изменения той или иной величины допущена ошибка, пользователю придется смириться с тем, что она выйдет за пределы поля построения графика. В любом случае, ошибка в определении возможных интервалов изменения отображаемых переменных для программы интегрирования никак не отразится на полученных результатах, и в ходе их отображения пользователь всегда может представить результаты в удобном виде.
3.4. РЕЗЮМЕ
1. Текст программы на языке PRADIS готовится с помощью обычного текстового редактора и состоит из двух частей: описания объекта и описания задания.
2. В разделе описания объекта с заголовком $ FRAGMENT содержится описание структуры объекта, описание закрепления фрагмента и описание вывода для фрагмента.
3. Подготовка расчетной модели включает в себя этапы определения системы координат и размерности физического пространства, в котором движется модель, декомпозиции объекта на элементы, выбора моделей элементов, представляющих тот или иной элемент объекта, описания структуры модели, описания вывода.
4. В разделе описания структуры задается описание соединения выбранных моделей элементов в соответствующих степенях свободы объекта (узлах) и определяются параметры этих элементов.
5. Описание вывода осуществляется с помощью вызова соответствующих программ расчета выходных переменных.
6. Описание задания состоит из описания задания на расчет (раздел RUN) и описания задания на отображение результатов (раздел PRINT).
7. Выполнение повторных заданий для уже сформированной модели можно осуществлять без выполнения этапов, связанных с новым формированием модели. Для этого используют команду запуска задания на уже сформированную модель. Например:
> SLANG T TEST
7. Для продолжения расчета с того места, на котором он был закончен в последний раз, используется заголовок $ RESTORE. Выполнение задания для уже сформированной модели без заголовка $ RESTORE ведет к расчету с начального момента времени и утрате данных предыдущего расчета.
8. К хорошему стилю написания программ на входном языке PRADIS относится:
а) обязательное именование фрагментов, составляющих описание объекта;
б) перечисление для программы интегрирования списка отображаемых в ходе расчета переменных с указанием соответствующих масштабов.
4. ВЫВОД И ОТОБРАЖЕНИE РЕЗУЛЬТАТОВ
Итак, мы рассмотрели колебания простейшего пружинного маятника и вывели на печать изменение скорости и перемещения груза с течением времени. При этом описание вывода обсуждалось не слишком подробно, лишь в той мере, в которой это было необходимо для решения простейшей задачи.
В этой главе хотелось бы подробнее остановиться на возможностях вывода в комплексе PRADIS. Выяснить, каким образом можно рассчитать и вывести на печать какие-либо другие характеристики объекта. Изучить возможности программ отображения (DISP).
Здесь мы будем пользоваться уже сформированной раньше моделью пружинного маятника, изменяя и дополняя соответствующие разделы программы.
4.1. ОРГАНИЗАЦИЯ ВЫВОДА РЕЗУЛЬТАТОВ В КОМПЛЕКСЕ PRADIS
В ходе расчета переходного процесса на каждом шаге интегрирования вычисляются текущие значения большого количества переменных. Для задач механики это:
- перемещения, скорости и ускорения по всем степеням свободы объекта;
- усилия и моменты, действующие на элементы по всем степеням свободы элементов;
- другие переменные, подсчитываемые моделями элементов. Модель элемента в общем случае содержит рабочий массив (рабочий вектор). В этом массиве могут храниться такие переменные, как энергия, поглощенная элементом, величина продольного или поперечного усилия, напряжение в элементе, потенциальная энергия деформации элемента и др.
Все перечисленные величины называются внутренними переменными. Обычно количество внутренних переменных велико, поэтому информация о них после выполнения расчета не сохраняется. Как и другие данные, они хранятся в массиве состояния расчета, содержимое которого обновляется на каждом шаге интегрирования.
В конкретной задаче пользователя может интересовать лишь некоторое количество выходных характеристик (чаще всего их много меньше, чем внутренних переменных). Кроме того, часто внутренняя переменная является лишь промежуточным результатом для получения требуемой выходной характеристики объекта. Поэтому принято, что пользователь должен сам для своей задачи определить необходимый ему состав рассчитываемых выходных характеристик. Помимо определенного пользователем состава вывода никаких данных по результатам расчета (кроме статистики программы интегрирования) не сохраняется.
Для расчета требуемых выходных характеристик используются Программы Расчета Выходных Переменных (ПРВП). В качестве исходных данных в такую программу передаются необходимые внутренние переменные и требуемые для ее работы постоянные параметры, задаваемые пользователем. Результатом ее работы является вычисление одной или нескольких выходных переменных. Полученные выходные переменные сохраняются в файле результатов расчета. Часть из них может отображаться по ходу интегрирования в виде графиков на экране дисплея.
Простейшие ПРВП просто переписывают значение соответствующей внутренней переменной в вектор выходных переменных. В общем случае проводятся более сложные расчеты, в которых используется несколько внутренних переменных и вычисляется несколько выходных переменных. Файл результатов расчета остается на диске после завершения вычислений и может быть использован в дальнейшем анализе – для продолжения расчетов, а также для отображения или постпроцессорной обработки результатов.
На каждом шаге интегрирования для расчета выходных переменных используется некоторое количество внутренних переменных. Пользователь, определившись предварительно со списком интересующих его выходных переменных и выбрав подходящие для их расчета ПРВП, должен указать, какие именно внутренние переменные будут использованы для расчета выходных характеристик.
Для этой цели (т.е. для указания на соответствующие внутренние переменные) в комплексе PRADIS используются указатели на внутренние переменные. Различают указатели трех типов.
Первый тип указателя – указатель на потенциальные характеристики узла (в механике – кинематические характеристики узла: перемещение, скорость, ускорение).
Второй тип указателя – указатель на потоковую переменную (в механике – на силовую переменную: усилие или момент).
Третий тип указателя – указатель на элемент рабочего вектора модели элемента.
Для каждой ПРВП задается список указателей на соответствующие внутренние переменные. Причем, количество передаваемых в ПРВП указателей на внутренние переменные и их тип определяется описанием соответствующей ПРВП. В некоторые ПРВП можно передавать указатели различных типов, для других ПРВП тип передаваемого этой программе указателя строго определен.
4.2. НЕКОТОРЫЕ ПРОГРАММЫ РАСЧЕТА ВЫХОДНЫХ ПЕРЕМЕННЫХ
В базовой библиотеке программ расчета выходных переменных комплекса PRADIS имеется некоторое количество программ расчета выходных переменных. Состав библиотеки ПРВП постоянно изменяется за счет появления новых программ. Поэтому целью этого подраздела является не детальное знакомство с базовой библиотекой ПРВП, а рассмотрение различных разновидностей ПРВП на примере нескольких программ. Такими разновидностями ПРВП являются
· программы, выводящие значения внутренних переменных комплекса (например, S, V и A). Как правило, в такие ПРВП передается одна внутренняя переменная определенного типа;
· программы с фиксированным количеством передаваемых в них внутренних переменных, использующие эти переменные как промежуточные результаты для расчета требуемых величин;
· ПРВП с переменным количеством передаваемых в них внутренних переменных, использующие эти переменные как промежуточные результаты для расчета требуемых величин.
Каждая из этих разновидностей ПРВП может рассчитывать вектор из нескольких выходных переменных.
4.2.1. Программы S, V, A и X
Основной и наиболее часто используемой программой расчета выходных переменных в комплексе PRADIS является программа S. В простейшем случае с помощью этой программы можно вывести величину перемещения для любого узла объекта. Для этого в качестве указателя на внутреннюю переменную используется номер соответствующего узла (указатель первого типа). Вывод перемещения 1-го узла в той системе единиц, которая используется для расчета (в нашем случае – в метрах), выглядит следующим образом:
Перемещение 'S (1; 1.0)
Как видно из приведенного примера, указатель на передаваемую внутреннюю переменную задается в скобках на первом месте (до разделителя;). После разделителя для программы S задается величина масштаба преобразования внутренней переменной в выходную. В приведенном вызове указан масштаб преобразования внутренней переменной, равный 1 (т.е., вывод величины перемещения в той же системе единиц, в которой проводился расчет – в метрах). Если в том же примере потребовался бы вывод перемещения в миллиметрах, то такой же вызов программы расчета выходной переменной выглядел бы по-другому:
Перемещение 'S (1; 1000)
Для вывода скорости или ускорения используются соответственно программы V и A. При этом в ПРВП в качестве указателя на внутреннюю переменную также передается номер узла, для которого выводится требуемая кинематическая характеристика. В качестве примера приведем вызов программы расчета выходной переменной V для вывода скорости узла 1 в километрах в час (масштаб преобразования 3.6) и программы A для вывода ускорения в м/с2:
Скорость узла 1' V (1; 3.6);
Ускорение узла 1' A (1; 1)
Итак, для вывода какой-либо кинематической характеристики в программу расчета выходных переменных передается номер узла объекта, для которого эта характеристика выводится. Какая именно характеристика будет выводиться, зависит от используемой ПРВП. Программа S используется для вывода перемещения, V – скорости, A – ускорения.
Небольшое лирическое отступление по поводу использования тех же ПРВП в других предметных областях. Одни и те же вызовы
S 'S (5; 1); U 'V (5; 1); W 'A (5; 1)
приведут к расчету для узла объекта с номером 5 в той системе единиц, в которой проводился расчет:
- для электрических задач – интеграла от потенциала ("S"), потенциала ("U") и его первой производной по времени ("W");
- в гидравлических и пневматических задачах – интеграла давления, давления и его производной по времени;
- в тепловых задачах – интеграла от температуры, температуры и ее производной по времени.
Завершая разговор о программах V и A, нужно сказать, что они могут быть использованы только для вывода тех характеристик, о которых говорилось выше. Т.е., в задачах механики – для вывода скорости и ускорения. Таким образом, в качестве указателей на внутренние переменные для программ V и A можно использовать только указатели первого типа.
Программа X является более универсальной и может быть использована для вывода любых внутренних переменных – усилий, моментов и переменных, рассчитываемых моделями элементов. Для вывода величины усилия или момента используется указатель на силу (указатель второго типа). Так, вывод величины усилия, действующего на пружину со стороны точечного инерционного элемента, в нашей задаче выглядел бы следующим образом:
Усилие 'X (I:Пружина(2); 1)
В этом вызове признак "I:" говорит о том, что в программу расчета выходной переменной X передается указатель на силу, действующую на элемент с идентификатором "Пружина" по второй ветви этого элемента (т.е., ветви, соединенной с узлом 1). Этот вызов приведет к выводу усилия, действующего на элемент "Пружина" и измеряемого в Ньютонах. В задачах механики для определения указателя второго типа можно использовать также признак указателя "F:". Так, для вывода той же переменной в килоньютонах (масштаб преобразования 0.001), можно было бы применить такой вызов:
Усилие в кН 'X (F:Пружина(2); 1E-3)
Использование этих же признаков указателя ("I:" или "F:") в задачах механики вращательного движения приведет к передаче в ПРВП момента для соответствующей ветви элемента. В других предметных областях признак указателя "I:" используется для формирования указателя на потоковую переменную, характерную для этой предметной области – силу тока, расход, тепловой поток. Для определения теплового или массового потока иногда полезно бывает использовать признак указателя "Q:".
Необходимо заметить, что указатели "I:Элемент 1(2)", "F:Элемент 1(2)" и "Q:Элемент 1(2)" полностью эквивалентны. Их использование приведет к передаче в ПРВП потоковой переменной для второй ветви элемента с идентификатором "Элемент 1". Существование различных признаков указателя для потоковой переменной ("I:", "F:" и "Q:") во входном языке комплекса PRADIS объясняется тем, что для различных предметных областей традиционно приняты определенные обозначения потоковых переменных. Ток в электронике обозначается буквой I, сила в механике – буквой F, поток в гидравлике или термодинамике – буквой Q. Поэтому для инженера, решающего, скажем, задачи механики, может показаться удобным использовать для формирования указателя второго типа признак указателя "F:". Для гидравлика – Q и т.д.
Оправданным является и такой подход, при котором для всех предметных областей потоковая переменная обозначается стандартно и одинаково. Авторы, как правило, используют во всех задачах универсальный признак указателя "I:" (это принято и дальше в этом пособии). Все не согласные и не очень согласные с этим подходом могут принять свои правила.
Как уже говорилось выше, для каждой модели элемента могут быть определены переменные, также относящиеся к внутренним переменным комплекса и доступные для передачи в программы расчета выходных переменных. Это переменные, входящие в состав рабочего вектора модели. Для каждой модели наличие таких переменных определено в ее описании. Так, согласно описанию, в модели элемента K имеется одна рабочая переменная – величина энергии, накопленная элементом. Для указания на элемент рабочего вектора используется признак W (этот признак определяет указатель третьего типа). В нашей задаче вывод энергии, накопленной пружиной, осуществляется следующим вызовом:
Энергия деформации пружины 'X (W:Пружина(1); 1)
Здесь задается вывод первого элемента рабочего вектора для модели элемента "Пружина" в системе единиц, в которой проводился расчет. Попытка вывода для элемента "Пружина" второго элемента рабочего вектора
Некая рабочая переменная 'X (W:Пружина(2); 1)
приведет к выводу величины, к элементу "Пружина" никакого отношения не имеющей. Кроме того, как уже было сказано выше, попытка использования для вывода элемента рабочего вектора модели программ V или A лишена смысла, так как эти программы предназначены только для вывода значения скорости и ускорения узла (или их аналогов в системах другой физической природы).
Пользователь, внимательно изучивший описание языка, в этом месте может сказать, что еще не были упомянуты две возможных разновидности указателей на внутреннюю переменную – номер узла с символом ' и номер узла с символом ". И такому пользователю мы прямо скажем: "Да. Не были". Поэтому помянем здесь.
Если в качестве указателя на внутреннюю переменную в тексте PRADIS-программы используется просто номер узла, то в соответствующую ПРВП передается вектор из трех переменных, первым элементом которого является перемещение, вторым – скорость, третьим – ускорение. Программа X переписывает в вектор выходных переменных первую из переданных ей переменных. Поэтому в этом случае, как мы видели выше, она выведет перемещение для узла с указанным номером. Использование в качестве указателя на внутреннюю переменную номера узла с символом ' приведет к передаче в программу вектора из двух переменных, первым из которых будет скорость. В этом случае программа X выведет скорость. Использование номера узла с символом " приведет к выводу ускорения. Таким образом, для нашего задания на анализ вывод скорости и ускорения узла 1 мог бы быть осуществлен и вторым способом:
Скорость узла 1' X (1'; 3.6);
Ускорение узла 1' X (1"; 1)
Такие указатели, как 1' и 1", используются для передачи в ПРВП потенциальной переменной (скорости и ускорения), поэтому они относятся к указателям ПЕРВОГО типа.
4.2.2. Программы расчета выходных переменных, использующие внутренние переменные комплекса в качестве промежуточных величин для расчета выходной переменной
Во многих случаях внутренние переменные, получаемые на каждом шаге интегрирования (они перечислены в начале главы), являются только промежуточными для получения окончательных выходных характеристик. Тогда имеет смысл выводить не непосредственно внутренние переменные, а использовать другие программы расчета выходных переменных комплекса PRADIS для преобразования внутренних переменных в соответствующие выходные переменные.
В качестве примера дополним нашу программу расчетом работы силы и мощности силового воздействия на массу со стороны источника постоянного усилия. Для этого можно использовать программы расчета выходных переменных N и W. Их вызов немного сложнее, чем для программ, описанных в предыдущем пункте, и авторы не помнят досконально все особенности вызовов этих программ. Для получения краткой справки воспользуемся встроенным HELP'ом:
> ARM ? N W
Те места файла SYSPRINT.TXT, которые интересуют нас в этом случае, выглядят следующим образом:
...
НАЗВАНИЕ: Программа расчета смасштабированного значения
мощности силового воздействия.
ТИП УКАЗАТЕЛЕЙ НА ПЕРЕДАВАЕМЫЕ В ПРОГРАММУ ВНУТРЕННИЕ ПЕРЕМЕННЫЕ:
1 - номер узла, к которому приложено силовое воздействие;
2 - указатель на силу (момент), мощность воздействия которой на
указанный узел требуется вычислить.
ПАРАМЕТРЫ :
1 - масштаб.
ВЫХОДНЫЕ ПЕРЕМЕННЫЕ:
1 - мощность силового воздействия (произведение силы на
скорость), умноженное на масштаб.
...
НАЗВАНИЕ: Программа расчета смасштабированного значения работы
силы (момента) на перемещении указанного узла.
ТИП УКАЗАТЕЛЕЙ НА ПЕРЕДАВАЕМЫЕ В ПРОГРАММУ ВНУТРЕННИЕ ПЕРЕМЕННЫЕ:
1 - номер узла, к которому приложено силовое воздействие;
2 - указатель на силу (момент), работу которой на перемещении
указанного узла требуется вычислить.
ПАРАМЕТРЫ:
1 - масштаб.
ВЫХОДНЫЕ ПЕРЕМЕННЫЕ:
1 - работа силового воздействия, умноженная на масштаб.
Первый из приведенных фрагментов файла SYSPRINT.TXT относится к программе N, второй – к W.
Из полученной информации видно, что для каждой из этих программ требуется задание двух указателей на внутренние переменные: указателя на номер узла, кинематические характеристики которого будут использованы для расчета, и указателя на соответствующую потоковую переменную (силу или момент). При этом существенно важным является порядок задания этих переменных. Первым обязательно задается номер узла, вторым – указатель на силу. В нашем случае вызовы программ расчета выходных переменных для расчета мощности силового воздействия со стороны источника постоянной силы в киловаттах и работы, производимой постоянной силой, в Джоулях, выглядят следующим образом:
Мощность силового воздействия ' N (1, I:Сила тяжести(1);0.001)
Работа силы ' W (1, I: Сила тяжести(1); 1)
4.2.3. Программы с переменным количеством указателей на внутренние переменные и программы, рассчитывающие несколько выходных переменных.
В базовой библиотеке PRADIS имеется некоторое количество ПРВП, в которые может передаваться несколько указателей на внутренние переменные. Примером такой программы может служить программа определения максимального значения из N внутренних переменных – MAXI. Например, в одном и том же задании можно использовать такие вызовы программы MAXI:
Максимальное значение силы' MAXI (I:Пружина 1,
I:Пружина 2; 1)
Максимальное перемещение ' MAXI (1, 2, 3, 4, 5; 1)
Как видно из приведенного примера, в первом случае определяется максимальное значение из двух внутренних переменных, а во втором – из пяти. Специально отметим, что такое возможно не для любой ПРВП. Возможность задания переменного количества указателей на внутренние переменные при вызове ПРВП специально оговаривается в описании программы. Так, для уже использованных в нашем примере ПРВП (S,V,A,X,W,P), эта возможность отсутствует.
У программы расчета выходной переменной MAXI есть еще одна особенность. Она рассчитывает не одну выходную переменную, а две. Говорят, что рассчитываемая с помощью программы MAXI выходная переменная является многокомпонентной (в данном случае – двухкомпонентной). Первая компонента – это максимальное значение из тех переменных, которые были переданы в программу, а вторая – порядковый номер этой переменной в списке указателей, передаваемых в программу.
Для той части квалифицированных расчетчиков, кто не программировал много, отметим, что эта программа может отвечать также на вопросы, типа: "Что больше – сила или перемещение?". Эта почти волшебная возможность может быть обеспечена вызовом
Что больше ' MAXI (I:Пружина(1), 1;1)
Задавший этот вопрос в любой момент может не только знать максимальное значение, выбранное из силы и перемещения, но и четко решить вопрос, что же все-таки из них максимально – сила (вторая компонента переменной "Что больше" равна 1), или перемещение (вторая компонента переменной "Что больше" в этом случае будет равна 2).
4.3. ПРОГРАММЫ ОТОБРАЖЕНИЯ РЕЗУЛЬТАТОВ РАСЧЕТОВ
Исходя из мысли, что мало заставить PRADIS посчитать, нужно уметь заставить его вывести посчитанное в удобном для пользователя виде, пройдемся здесь также по возможностям отображения получаемых результатов расчета.
4.3.1. Оперативное отображение выходных переменных в ходе расчета
Когда количество выходных переменных в задании невелико (меньше 5), при вызове программы интегрирования перечислять отображаемые переменные не обязательно. В этом случае по ходу расчета будут отображаться все выходные переменные. Однако, в реальных задачах количество выходных переменных может быть большим, и тогда все они на экране могут не уместиться. Обычно, для визуального контроля хода расчета это и не обязательно. В таком случае нужно выбрать две-три наиболее представительных переменных, которые характеризуют основные параметры процесса, и вывод которых на экран дает наибольшее количество полезной информации. Остальные переменные будут доступны для отображения после окончания расчета. Если для расчета процесса используется несколько программ интегрирования, то в каждой из них можно описать свой набор отображаемых переменных.
Учитывая вышесказанное, для оперативного отображения в нашей задаче можно оставить силу и перемещение, сохранив те же масштабы вывода.
Если оперативный вывод информации не определен пользователем, а в программе задан расчет большого количества выходных переменных, то программа интегрирования не будет себя особо утруждать размышлениями о том, какие из выходных переменных нужно отображать в ходе расчета. При этом будут отображаться любые выходные переменные в том порядке, в котором это будет удобно программе интегрирования. Поэтому стоит еще раз напомнить, что хорошим стилем программирования на языке PRADIS является перечисление для программы интегрирования списка отображаемых по ходу расчета переменных с указанием соответствующих нижнего и верхнего ограничения этих величин.
4.3.2. Программы символьного отображения результатов расчета
В стандартной версии комплекса имеется программа отображения, позволяющая оперативно выводить информацию о результатах расчета на АЦПУ. Это программа вывода информации о результатах расчета в виде таблицы – TABL. Ее достоинством по сравнению с другими программами отображения является то, что она позволяет для любого момента времени получить точное численное значение нужной величины (значение величины, полученное из графика, при любом способе построения графика будет менее точным). Как и для всех остальных программ расчета и отображения, управляющая информация для нее задается в виде ключевых параметров. Для получения справки заглянем в справочник по системе или, как и раньше, введем команду
>ARM ? TABL
Наиболее интересный для нас сейчас участок файла SYSPRINT.TXT имеет вид:
...
НАЗВАНИЕ: Программа отображения результатов в виде
таблицы значений выходных переменных.
КЛЮЧЕВЫЕ ПАРАМЕТРЫ:
START - начальный момент времени;
END - конечный момент времени;
OUT - шаг вывода по времени;
FORMF - флаг управления форматом вывода:
при FORMF=1 формат вывода с фиксированной точкой.
ОГРАНИЧЕНИЯ:
Максимальное количество выходных переменных - 14
ТРЕБУЮЩИЕСЯ УСТРОЙСТВА: Не требуются.
...
Итак, для управления работой программы TABL можно пользоваться четырьмя ключевыми параметрами. С помощью параметров START и END задается требуемый временной интервал вывода. Если эти параметры не заданы, выводится весь рассчитанный для процесса временной интервал. Параметр OUT управляет шагом вывода информации по времени. Его действие аналогично действию соответствующего параметра GRAFCH. Отличие заключается в значениях, принимаемых для него по умолчанию и в действиях программы, когда величина OUT превосходит разницу между начальным и конечным моментом времени для выводимого интервала (END – START). Для GRAFCH по умолчанию принимается OUT=0.1, а в случае, если OUT > END – START, то будет выведена только одна строка графика. Для TABL величина ключевого параметра OUT, принимаемая по умолчанию, OUT=1.E10, а в случае, если OUT > END – START, то будет выведена только шапка таблицы результатов – экстремальные значения отображаемых переменных на заданном временном интервале. Вывод числовых значений времени и выходных переменных осуществляется в формате с плавающей точкой. Часто удобнее и нагляднее представлять числа в формате с фиксированной точкой. Для этого используется флаг управления форматом печати FORMF. Если задано FORMF=1, то вывод числовых значений осуществляется по формату, соответствующему формату FORTRAN’а F12.6 (всего для представления числа используется 12 позиций, из них 6 позиций – под представление дробной части). В случае, если этого поля для представления числа будет недостаточно, то на его месте выводятся символы "*".
В справочной информации говорится также, что программа TABL может вывести в одну таблицу не более 14 отображаемых переменных.
Используем эту программу в нашем примере для отображения величины накопленной пружиной энергии и соответствующего этой энергии перемещения:
Растяжение и энергия пружины 'TABL START=0,END=1,OUT=0.01;
Перемещение,
Энергия деформации пружины)
Заметим, что для программы TABL не нужно задавать нижнее и верхнее ограничения на интервал отображения выходной переменной. Поэтому, если они будут заданы, получим сообщение о синтаксической ошибке.
4.3.3. Отображение результатов расчета в виде графиков на экране дисплея.
Если ваша вычислительная установка имеет графический экран, то скорее всего основной программой отображения, которой вы будете пользоваться, станет программа отображения результатов расчета в виде графиков на экране дисплея – DISP.
Эта программа имеет 3 ключевых параметра. Значения параметров START и END имеют тот же смысл, что и для программы TABL. Параметр OUT в данном случае отсутствует, так как шаг вывода определяется разрешением имеющегося у Вас экрана дисплея и полученными в ходе расчета результатами. Зато для программы DISP имеется еще один ключевой параметр, с которым мы ранее еще не встречались. В некоторых случаях нужно получить графики тех или иных величин в зависимости не от времени, а от другой выходной переменной. Для этой цели используется параметр FROM. Этот параметр задает порядковый номер той выходной переменной из списка, указанного при описании вызова программы, в зависимости от которой требуется строить графики остальных переменных. Если этот параметр не задан или задано FROM=0, то графики строятся в зависимости от времени.
Зададим в нашей программе два вызова программы отображения DISP. В первом вызове определим отображение полученных кинематических характеристик маятника – перемещения, скорости и ускорения, а также энергии деформации пружины. При этом график перемещения выведем в двух разных масштабах (один из масштабов позволит рассмотреть общий вид графика, а второй – его поведение вблизи максимума перемещения):
Результаты расчета N1'DISP (;
Перемещение = (0, 2),
Перемещение = (1.9,2),
Скорость = (-5,5),
Ускорение ,
Энергия деформации пружины)
Во втором вызове получим график зависимости скорости груза, мощности и работы источника постоянного усилия в зависимости от величины перемещения:
Результаты расчета N2' DISP ( FROM=1;
Перемещение = (0, 2),
Скорость = (-5,5),
Мощность силового воздействия,
Работа силы)
В приведенных вызовах программ отображения заданы нижнее и верхнее ограничения интервала отображения для выходных переменных "Перемещение", "Скорость". Для переменных "Энергия деформации пружины", "Мощность силового воздействия" и "Работа силы" эти интервалы не заданы. Поэтому интервалы отображения этих величин будут выбраны программой отображения исходя из максимального и минимального значения величин, полученных в ходе интегрирования.
Нужно отметить, что вызов программы отображения DISP, как и вызов любой другой программы отображения, может быть осуществлен без определения списка отображаемых переменных. Тогда, если количество выходных переменных в программе не превосходит допускаемого данной программой количества отображаемых переменных, все они отображаются. В противном случае все программы отображения будут поступать так же, как и программа интегрирования. Т.е., будет отображено доступное для DISP количество выходных переменных. При этом выбор состава и порядка выводимых переменных остается за программой отображения. Поэтому, во избежание недоразумений и скандалов, в хорошей программе на языке PRADIS при вызове программ отображения желательно также всегда определять список отображаемых переменных. Иногда для большего удобства при работе с результатами или для их размещения в соответствующем месте на экране полезно задавать и масштабы изображения.
По горячим следам поднимем вопрос с отображением многокомпонентной выходной переменной (она обсуждалась в пункте 4.2.3). Допустим, что один из пользователей все же задал сакраментальный вопрос по поводу силы и перемещения (соответствующая выходная переменная называлась там "Что больше"). Тогда для вывода каждой из компонент этой переменной номер компоненты указывается в скобках после идентификатора:
Ответ на ВОПРОС 'DISP (;
Что больше (1), Что больше (2) = (1,2))
Обратите внимание, что пользователь, это написавший, обладает изрядной квалификацией. Это видно хотя бы из того факта, что для вывода второй компоненты переменной "Что больше" четко заданы нижняя и верхняя граница интервала отображения. Поскольку в нашем случае вторая компонента может принимать только значения 1 или 2, то ответ на заданный вопрос предельно упрощается. Если график второй переменной рисуется по нижней границе поля изображения графика – сила все еще больше, а уж если по верхней – то перемещение превосходит силу.
4.4. ПРОГРАММА РАСЧЕТА КОЛЕБАНИЙ МАЯТНИКА, ИСПОЛЬЗУЮЩАЯ БОЛЬШЕ ВОЗМОЖНОСТЕЙ ВЫВОДА ИНФОРМАЦИИ
Внесем некоторые из перечисленных выше изменений в программку анализа колебаний маятника. Вот что получилось у авторов:
$ FRAGMENT: Маятник
# BASE : 2
# STRUCT :
Пружина 'K (2,1; 10); Масса 'M (1; 1)
Сила тяжести 'F (1; 9.81)
# OUTPUT :
Перемещение 'S (1; 1);
Усилие 'X (I:Пружина(2); 1)
Скорость 'V (1; 1); Ускорение ' A (1; 1)
Энергия деформации пружины 'X (W:Пружина(1); 1)
Мощность силового воздействия 'N (1,I:Сила тяжести(1);0.001)
Работа силы ' W (1, I: Сила тяжести(1); 1)
$ RUN :
' SHTERM (END=2; Перемещение=(0,2),Скорость=(-5,5))
$ PRINT :
Результаты расчета N1'DISP (;
Перемещение = (0,2), Перемещение = (1.9,2),
Скорость = (-5,5), Ускорение = (-100,100),
Энергия деформации пружины)
Результаты расчета N2'DISP (FROM=1; Перемещение = (0,2),
Скорость = (-5,5), Мощность силового воздействия,
Работа силы)
Растяжение и энергия пружины 'TABL (START=0,END=1,OUT=0.01;
Перемещение, Энергия деформации пружины)
$ END
Новый текст программы на языке PRADIS мы поместили в файл TEST2. Запуск задания на выполнение анализа по новой программе выполняется уже знакомой нам командой
>SLANG TEST2
На этот раз по ходу интегрирования будут отображаться перемещение и скорость маятника. После интегрирования два раза отработает программа DISP, построив на экране зависимости требуемых выходных переменных от времени и от перемещения маятника. Программа TABL результаты своей работы оставит в файле TEST2.GRF. Этот файл можно просмотреть с помощью текстового редактора и распечатать на АЦПУ.
В заключение хотелось бы отметить еще один момент, который остался за рамками обсуждения в предыдущей главе. Речь идет о возможности выполнять задание на отображение результатов, сохраненных в файле результатов расчета, без повторного выполнения анализа.
Допустим, некоторому любознательному пользователю приспичило в порядке эксперимента уже после выполнения задания для TEST2 построить зависимости перемещения, мощности и работы от скорости движения груза. Чтобы было еще интереснее, ограничим временной интервал вывода промежутком времени 0.5...1.5 с и определим для скорости другие масштабы. В этом случае не требуется выполнять повторный анализ (что несущественно для рассматриваемой задачи, но может оказаться существенным для более крупных задач). Тогда этот гипотетический любознательный молодой человек вслед за авторами имеет возможность сформировать программку, содержащую задание на отображение результатов:
$ PRINT :
Результаты расчета N2'DISP (FROM=2; Перемещение = (0,2),
Скорость = (-5.731,5.7987 E-2), Мощность силового
воздействия, Работа силы)
$ END
Поместив эту программку в файл с именем, скажем, SUPER, он имеет право воспользоваться командой
>SLANG SUPER TEST2
и далее получать эстетическое удовлетворение от результатов, представленных в другом виде (не так, как это было предусмотрено в тексте основного задания).
Эту возможность, кроме всего прочего, полезно использовать для "причесывания" результатов, которые в дальнейшем могут входить в отчет по работе. За счет подбора масштабов можно размещать графики тех или иных величин в нужном месте используемого программой поля, "раздвигать" часто пересекающиеся графики, изображать более крупно выбранные временные отрезки, изменять состав переменных, выводимых на том или ином графике. Как показывает опыт, для серьезного расчета редко удается получить сразу все графики в виде, удобном для человека, не имевшего отношения к этой работе. Поэтому на заключительных этапах, уже после выполнения расчетов, обычно многократно выполняются задания на отображение результатов. По ходу этой работы "отлаживается" окончательный вид представления результатов.
4.5. РЕЗЮМЕ.
1. Весь вывод в комплексе PRADIS осуществляется с помощью программ расчета выходных переменных (ПРВП). Для расчета выходных переменных в каждую ПРВП требуется передать одну или несколько внутренних переменных, полученных рабочей программой в ходе расчета. Значения этих переменных используются в ПРВП для расчета требуемых выходных характеристик. В простейшем случае значение внутренней переменной просто переписывается в вектор выходных переменных.
2. Значения всех полученных выходных переменных сохраняются в файле результатов расчета. Этот файл остается на магнитном носителе после выполнения расчета и может быть многократно использован для той или иной постпроцессорной обработки результатов и их отображения.
3. Для передачи в ПРВП внутренних переменных используются указатели на внутреннюю переменную. В зависимости от типа передаваемой в ПРВП внутренней переменной различают указатели нескольких типов. Нами были рассмотрены следующие типы указателей:
- указатель на потенциальную (в механике – кинематическую) характеристику узла. В качестве указателя на потенциальную характеристику узла используются номер узла, номер узла с символом ' и номер узла с символом ". В первом случае в ПРВП передается весь вектор потенциальных переменных для узла (в механике – перемещение, скорость и ускорение), во втором – вектор потенциальных переменных, начиная с первой производной основной потенциальной переменной по времени (в механике – скорость и ускорение), в последнем случае – вторая производная основной потенциальной переменной по времени (в механике – ускорение). С точки зрения получаемого результата следующие описания выходных переменных эквивалентны:
Скорость 'V (3; 1) и Скорость 'X (3';1)
Ускорение'A (3; 1) и Ускорение'X (3";1)
- указатель на потоковую переменную (в механике – указатель на силу или момент). Для определения указателя на потоковую переменную используется признак I:. После него задается идентификатор элемента и, в круглых скобках, номер ветви этого элемента, которой соответствует требуемая внутренняя переменная;
- указатель на элемент рабочего вектора модели элемента. Для определения указателя на элемент рабочего вектора применяется признак W:. После него задается идентификатор модели элемента и порядковый номер требуемой переменной в рабочем векторе. Содержимое рабочего вектора для каждой модели элемента, если этот вектор имеется в данной модели, описано в справочной информации;
4. В комплексе PRADIS имеется некоторое количество ПРВП с переменным количеством указателей на внутренние переменные, а также – ПРВП, рассчитывающие многокомпонентные выходные переменные. Для отображения отдельных компонент многокомпонентной выходной переменной в списке отображаемых переменных для программы интегрирования и программы отображения задается идентификатор переменной и, в скобках, номер соответствующей компоненты.
5. Выходные переменные, сохраненные в файле результатов расчета, можно подвергать многократному отображению. В этом смысле произвол пользователя ограничен только составом включенных в комплекс программ отображения и его личным временем. Каждый уважающий себя пользователь PRADIS стремится выполнить только один расчет, а затем заниматься отображением.
6. Количество доступных для одновременного отображения выходных переменных зависит от используемой программы отображения. Так, TABL может строить таблицу одновременно для 14 переменных, в то время как для DISP количество доступных для одновременного отображения переменных в зависимости от типа используемого монитора может колебаться в пределах от 5 до 8.
7. Традиционная рубрика "Хорошего тона". Здесь одна рекомендация: указывайте для каждой программы отображения состав отображаемых при данном вызове выходных переменных.
5. АНАЛИЗ БОЛЕЕ СЛОЖНОЙ ЗАДАЧИ
Начиная с этой главы, мы будем рассматривать возможности комплекса, связанные с анализом более сложных объектов, состоящих, как правило, из нескольких фрагментов. В первом подразделе вводятся средства описания данных комплекса PRADIS и, соответственно, возможности замены параметров на примере модели из предыдущих разделов. Дальнейший материал излагается для более сложной задачи, описанной в подразделе 5.2.
5.1. РАЗДЕЛ ОПИСАНИЯ ДАННЫХ И СРЕДСТВО ЗАМЕНЫ ПАРАМЕТРОВ
Как мы видели в предыдущих главах, параметры моделей элементов и программ расчета выходных переменных в программе на языке PRADIS можно задавать непосредственно в тексте описания объекта. Еще одна возможность описания данных в PRADIS-программе – это использование разделов описания данных (DATA). В этих разделах могут быть предварительно определены списки параметров, которые в дальнейшем используются в разделе описания объекта для задания параметров моделей элементов, фрагментов, программ расчета выходных переменных.
В нашем простейшем случае раздел описания данных и раздел описания объекта могли бы выглядеть следующим образом:
$ DATA :
Жесткость = 10; Масса тела = 1;
Величина силы тяжести = 9.81;
Масштаб перемещений = 1; Масштаб ускорений = 1;
Масштаб скоростей = 1; Масштаб энергии = 1;
Масштаб усилий = 1; Масштаб мощности = 0.001;
$ FRAGMENT: Маятник
# BASE : 2
# STRUCT :
Пружина 'K (2,1; Жесткость); Масса 'M (1; Масса тела)
Сила тяжести 'F (1; Величина силы тяжести)
# OUTPUT :
Перемещение 'S (1; Масштаб перемещений);
Усилие 'X (I:Пружина(2); Масштаб усилий)
Скорость 'V (1; Масштаб скоростей);
Ускорение ' A (1;Масштаб ускорений);
Энергия деформации пружины 'X (W:Пружина(1);
Масштаб энергии);
Мощность силового воздействия ' N (1, I:Сила тяжести(1);
Масштаб мощности);
Работа силы ' W (1, I:Сила тяжести(1); Масштаб энергии);
Использование сформированных в разделе описания данных списков параметров имеет один недостаток. Это, как правило, большие затраты на обдумывание и набивку текста программы, чем при использовании описанного в предыдущих разделах способа задания исходных данных (многие, в том числе и авторы, особенно те, кто в своей жизни попрограммировал, видимо усомнятся, является ли это недостатком). Преимущества – улучшилась читаемость текста программы и повысились удобства в ее исправлении. Теперь не нужно искать константу по всему тексту (а он может быть достаточно большим). Все задаваемые для программы параметры могут быть размещены в разделе описания данных.
Кроме этих, лежащих на поверхности, преимуществ, имеется еще одно. Все списки параметров, присутствующие явно в тексте описания объекта, становятся доступными для замены на последующих стадиях анализа. Для того, чтобы воспользоваться этой возможностью, внесем изменения в наш многострадальный TEST (в нем появится раздел DATA, а в разделе FRAGMENT при описании элементов и программ расчета выходных переменных будут присутствовать только списки параметров, определенные в разделе DATA, как это было показано выше). Запустим процедуру выполнения задания
> SLANG TEST
и дождемся завершения работы программы. Результаты должны быть такими же, как и для задания из предыдущей главы. Теперь проиллюстрируем, как этой моделью можно пользоваться в довольно распространенном на практике случае: когда требуется расчет нескольких вариантов для модели с одной и той же структурой, но разными параметрами элементов.
Допустим, нам нужно получить результаты анализа для нескольких вариантов процесса. Параметры элементов в каждом варианте, например, следующие:
Вариант 1. Масса груза 0.5 кг. Жесткость пружины 5 Н/м.
Вариант 2. Масса груза 0.5 кг. Жесткость пружины 10 Н/м.
Вариант 3. Масса груза 0.5 кг. Жесткость пружины 20 Н/м.
Как и прежде, для расчета любого из вариантов можно изменить параметры соответствующих элементов (в этом случае данные находятся в разделе DATA написанной выше программы) и выполнить команду
> SLANG TEST
Однако, в данном случае удобнее воспользоваться другой возможностью языка, а именно – возможностью замены параметров в уже сформированной модели. Для этого создадим файл с именем, скажем, REPL, содержащий следующую информацию:
$ REPLACE :
{ Данные для расчета варианта 1}
Масса тела = 0.5
Жесткость = 5
Величина силы тяжести = 4.905
$ RUN :
SHTERM (END=2; Перемещение=(0,2),Скорость=(-5,5))
$ PRINT :
Результаты расчета 'DISP (;
Перемещение = (0,2), Перемещение = (1.9,2),
Скорость = (-5,5), Ускорение = (-100,100),
Энергия деформации пружины)
$ END
Итак, задание для анализа первого варианта сформировано. Если вы не поленились и выполнили действия, описанные в начале этого подраздела, теперь можно рассчитать первый вариант командой.
> SLANG REPL TEST
Проанализировав результаты для первого варианта, можно в этом же файле задать данные для второго варианта и точно также выполнить его расчет. Необходимо отметить, что каждый вариант расчета воспринимается комплексом как анализ одного и того же объекта с именем TEST. Поэтому, анализ первого варианта приведет к автоматическому уничтожению результатов начального расчета, а анализ второго варианта – к уничтожению результатов расчета для первого варианта. Поэтому, выполняя многовариантный расчет, пользователь должен сам позаботиться о сохранении нужных результатов. Одна из возможностей – это сохранить файл с расширением .RSL (в нашем случае – TEST.RSL) под другим именем. Или для каждого интересующего пользователя варианта получить твердую копию полученных результатов. В крайнем случае, выписать в записную книжку максимальное значение силы, а максимальное значение скорости запомнить, повторив три или четыре раза и крепко зажмурив глаза (шутка).
Один совет. Никогда неизвестно, сколько раз придется выполнять расчет объекта и для каких сочетаний параметров. Может случиться, что какой-либо из параметров в тексте программы ошибочен. И всегда бывает огорчительно из-за пустяковой ошибки или недосмотра повторять задание с самого первого шага. Поэтому, как нам кажется, нужно взять за правило описывать все списки параметров в разделе DATA.
Нужно иметь ввиду еще один важный момент. Замена параметров с помощью REPLACE действует только по ходу текущего расчета (т.е., параметры в базе данных для сформированной модели не заменяются). Если в только что разобранном нами примере после выполнения одного или всех вариантов расчета удалить из файла REPL раздел REPLACE, то выполнение задания REPL для модели TEST приведет к расчету модели с первоначальными значениями параметров.
5.2. ОПИСАНИЕ БОЛЕЕ СЛОЖНОЙ ЗАДАЧИ (МОДЕЛИРОВАНИЕ ТЕХНОЛОГИЧЕСКОЙ МАШИНЫ)
Предлагаемый здесь в качестве "более сложной задачи" пример выбирался таким образом, чтобы он по возможности носил общеинженерный характер. При проектировании подавляющего большинства технических объектов инженер имеет дело с такими понятиями, как привод, двигатель, механизм (исполнительный механизм), нагрузка. Тем пользователям, которые сочтут для себя невозможным вникать (хотя бы даже и поверхностно, на уровне изложения в этом пособии) в "не относящиеся к их области деятельности проблемы", можно предложить пропустить те части пунктов 5.3.1 и 5.3.3, где речь идет о первичном обосновании выбора параметров тех или иных элементов.
Приступим к анализу предлагаемого объекта, изображенного на рис. 5.1. Это машина, выполняющая полезную работу с помощью ползуна. Ползун совершает возвратно-поступательное движение и преодолевает нагрузку P, которая зависит от его перемещения и действует на ползун только при его ходе вниз (обратный ход – холостой). Рабочий орган приводится в движение с помощью рычажного механизма, содержащего шатун, кривошип, коромысло и треугольный рычаг, шарнирно соединенный с первыми тремя звеньями. Коромысло, как ему и положено, совершает качающиеся движения (заставляет точку B двигаться вокруг точки E по дуге окружности). Движение механизма задается вращательным движением кривошипа, который, в свою очередь, жестко связан с зубчатым колесом редуктора. Предполагается, что синтез рычажного механизма, исходя из требуемой кинематики движения, уже проведен. Начальные координаты точек O, A, B, C, D, E (первая цифра – абсцисса, вторая – ордината в системе координат, связанной с точкой крепления ведущего кривошипа):
Точка O = 0., 0. ;
Точка A = -0.134, 0.238;
Точка B = 0.173, -0.109;
Точка C = 0.092, -0.339;
Точка D = 0.55, -0.95 ;
Точка E = 0.55, 0.
Как видно из начальных координат точек, механизм имеет эксцентриситет (т.е. точка D смещена от вертикальной оси, проходящей через т.O, на величину 0.55 м). Машина приводится в движение двигателем с линейной механической характеристикой. В начальный момент времени двигатель включается и разгоняет до некоторой угловой скорости ведущие части муфты сцепления. Через 6 секунд после включения двигателя начинается включение муфты. Усилие прижима дисков муфты задано и достигает максимальной величины в момент времени примерно 6.3 секунды после включения двигателя.
Вообще говоря, требуется выполнить проектный расчет, т.е. подобрать параметры конструктивных элементов, обеспечивающих выполнение заданной полезной работы. Учитывая рассматриваемую здесь тематику, расчет должен быть выполнен на основе динамического анализа.
Обычным в таких случаях подходом является предварительный расчет, в котором более или менее точно назначаются только некоторые известные параметры (параметры двигателя, технологической нагрузки, возможно, кинематика). Остальные величины, за неимением информации, задаются, исходя из опыта проектирования аналогов, здравого смысла или исходя из предельно допустимых, по мнению разработчика, величин. Например, в первом приближении, до определения действующих нагрузок, жесткость рычагов рассматриваемой конструкции может быть принята очень большой.
Результаты первого расчета служат для уточнения параметров рассматриваемой машины. Изменение параметров влияет на происходящие в объекте процессы. Поэтому, для получения работоспособного варианта конструкции требуется проведение нескольких последовательных уточняющих расчетов. По результатам каждого расчета принимаются решения об изменении тех или иных параметров.
|
|
|
|
Рис. 5.1. |
Кинематическая схема рычажного механизма и привода моделируемой машины |
Сформируем на основании такого подхода математическую модель рассматриваемой машины и пройдем несколько шагов по тому пути, который предложен в предыдущем абзаце.
5.3. ФОРМИРОВАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ТЕХНОЛОГИЧЕСКОЙ МАШИНЫ.
Описание объекта на входном языке комплекса PRADIS может содержать несколько разделов описания объекта (фрагментов). При этом считается, что полная структура анализируемого объекта представлена в ПОСЛЕДНИМ из них. Этот фрагмент носит название глобального фрагмента. Все остальные разделы описания объекта в задании на языке PRADIS предназначены для описания каких либо относительно независимых частей (или конструктивных узлов) исследуемого объекта. После описания этих фрагментов они могут быть использованы для формирования структуры глобального фрагмента как макроэлементы. Если такой макроэлемент включается в структуру формируемого глобального фрагмента, это значит, что в его структуру включаются все элементы включаемого фрагмента. Кроме того, весь список вывода для такого фрагмента попадает в общий список вывода глобального фрагмента. В случае, если какой-либо из фрагментов присутствует в тексте задания, но не включен в структуру глобального фрагмента, то для него проводится только синтаксический контроль текста. В дальнейшем информация о таких фрагментах игнорируется без каких-либо сообщений.
Правило фрагментации сложного объекта является универсальным. Не пытайтесь сразу построить сложную модель. Здесь, как и везде в программировании, принцип модульности и постепенности должен стоять на первом месте. Выделил несколько фрагментов, отладил их в отдельности, убедился, что все верно. Только после этого имеет смысл из отлаженных фрагментов формировать математическую модель всего объекта.
Пользователям, которых не удовлетворит по каким-либо причинам использование фрагментации, можно посоветовать еще один работоспособный метод формирования описания структуры сложного объекта. Это – постепенное усложнение анализируемой структуры. В этом методе на первом этапе формируется модель простейшего работоспособного объекта, являющегося частью анализируемого (в нашем случае, например, система двигатель-маховик), которая подвергается "отладке" (т.е., проводится расчет динамики и внимательный анализ результатов). После устранения всех замеченных в этом объекте ошибок к нему добавляется еще несколько элементов и расчет объекта повторяется. Чем меньше расчетного опыта у пользователя и чем менее однороден объект (чем больше разновидностей моделей элементов он включает), тем на большее количество этапов следует разбить этот процесс.
Дальше в этом документе рассматривается формирование модели сложного объекта из фрагментов, поскольку этот путь затрагивает большее количество элементов входного языка комплекса PRADIS. Это в любом случае полезно, даже если в дальнейшем пользователь решит пользоваться второй из описанных здесь технологий формирования сложных моделей.
Рисунок 5.1, по которому мы начинаем работать, специально скомпонован таким образом, что появляется желание выделить в объекте два фрагмента - привода и исполнительного механизма.
Итак, первый шаг сделан, и анализируемый объект разбит на две относительно независимых части (мы им дали имена "ПРИВОД" и "МЕХАНИЗМ"). Результаты этого шага мы изобразили на рис. 5.2. Поскольку пока внутренняя структура каждого из фрагментов не определена, неясно также, как их соединять. Поэтому приступим к определению структуры каждого из выделенных фрагментов.
5.3.1. Модель привода.
Как и в простейшей задаче, рассмотренной в 3 главе, осуществляем декомпозицию фрагмента привода на элементы (результаты этого шага представлены на рис. 5.3). Ниже приводится список выделенных в объекте элементов:
- основание, служащее для закрепления привода;
- двигатель с линейной механической характеристикой (DVLT, Двигатель);
- осевой идеально упругий элемент с двумя степенями свободы (K, - Участок вала N1, Участок вала N2);
- фрикционная муфта сцепления (MUFTA, Муфта сцепления);
- источник импульса силы трапециевидной формы (FTR, Усилие прижима);
- передаточное отношение с потерями (REDCT, Редуктор).
Заметим, что здесь крутильная жесткость участков вала представляется осевым идеально упругим элементом, таким же, каким в предыдущей программе моделировалась идеально упругая пружина. В данном случае это возможно (закон Гука для вращательного и поступательного движений имеют идентичную форму записи). Только в случае рассмотрения вращательного движения в качестве силового фактора фигурирует момент, а кинематическими характеристиками являются угол поворота, угловая скорость и угловое ускорение. В качестве параметра для этого элемента задается значение крутильной жесткости.
Как и в главе 3, получим более подробную справку (о количестве ветвей и параметров) для незнакомых нам элементов:
> ARM ? DVLT REDCT MUFTA FTR
Рассмотрим каждый из этих элементов несколько подробнее.
DVLT – двигатель с линейной механической характеристикой. Этот элемент имеет две степени свободы (поворот ротора двигателя и поворот корпуса двигателя). Параметры двигателя в том порядке, в котором они будут заданы в тексте описания объекта:
1) Пусковой момент двигателя в соответствии с рис. 5.1. – 10 Н*м.
2) Угловая скорость при нулевом моменте на валу двигателя – 50рад/с
|
|
|
|
Рис. 5.2. |
Декомпозиция исследуемой машины на фрагменты. |
3) Двигатель включается в момент времени 0 с.
4) Двигатель выключается в момент времени 1000 с (возьмем с запасом, чтобы двигатель не выключился в ходе работы машины)
5) Момент инерции вала двигателя (в нашей модели этот параметр будет учитывать инерцию всех подвижных частей, связанных с ротором двигателя). В задании параметр не определен. Учитывая, что максимальная мощность, развиваемая двигателем – 125 Вт, момент инерции вала двигателя не может быть очень большим. Зададим его величину 0.0025 кг*м2 (как у шкива массой 1 кг и диаметром 10 сантиметров).
6) Момент инерции корпуса двигателя. Корпус двигателя в модели будет неподвижен, поэтому величина этого параметра на расчеты не повлияет. Зададимся величиной 1 кг*м2.
REDCT – модель редуктора с учетом потерь на трение в зацеплении. Этот элемент также двухполюсник (поворот ведущей шестерни, поворот ведомого колеса). Параметры редуктора:
1) Величина передаточного отношения. Этот параметр можно определить ориентировочно, исходя из того, что полезная работа, совершаемая машиной за один цикл - 0.2*500 + 0.5*0.1*500 = 125 Дж (площадь под кривой "Сопротивление движению в зависимости от хода ползуна" на рис. 5.1). При работе с максимальной мощностью нашему двигателю на выполнение этой работы потребуется 1 секунда. Тогда угловая скорость выходного вала редуктора должна быть 6.28 рад/с. Предполагая, что двигатель обеспечивает угловую скорость движения 25 рад/с
(режим, соответствующий максимальной мощности двигателя), получим величину передаточного отношения редуктора U = 25/6.28 = 3.98. Окончательно остановимся на передаточном отношении 4.
2) Коэффициент полезного действия зубчатого редуктора при номинальном моменте принимаем 0.96.
3) Номинальный момент на шестерне редуктора. Этот параметр влияет на характер потерь в редукторе. Чем больше номинальный момент и меньше действительная величина нагрузки, тем выше относительные потери в редукторе. Максимальный момент, который воздействует на шестерню редуктора, в какой-то степени определяется максимальным моментом, развиваемым двигателем. Если исходить из этих соображений, то номинальный момент зубчатого редуктора – 10 Н*м.
4) Жесткость передачи, приведенная к первому колесу. Этот параметр до определения геометрии зацепления назначить затруднительно. Поэтому, предлагается величина, заведомо превосходящая реализуемую на практике. Скажем, 1 * 109Н*м/рад.
5) Момент инерции шестерни зададим соизмеримым с моментом инерции вала двигателя. Например, 0.005 кг*м2.
6) Момент инерции колеса, исходя из передаточного отношения и заданного момента инерции шестерни, примерно 0.005 * 42 = 0.08 кг*м2.
MUFTA – модель фрикционной муфты включения. Эта модель – трехполюсник (вращения ведущих и ведомых частей муфты, перемещение нажимного элемента). Параметры муфты:
1) Жесткость возвратных пружин. Эта величина должна согласовываться с величиной усилия прижима на нажимном элементе и номинальным (свободным) ходом нажимного элемента (четвертый параметр этой модели). Принимая свободный ход нажимного элемента 0.005 м и предполагая, что на преодоление усилия возвратных пружин затрачивается 10 % от максимального усилия прижима, получим величину жесткости возвратных пружин:
Kv = 0.1*500 / 0.005 = 50 000/5 = 1*104 Н*м.
2) Осевая контактная жесткость полумуфт. Эта величина является неопределенной, но должна быть значительно большей, чем жесткость возвратных пружин. Считая, что контактная деформация полумуфт составляет 10 % от свободного хода нажимного элемента и учитывая, что 10 % усилия прижима уже уравновешены возвратными пружинами, принимаем ориентировочную контактную жесткость полумуфт
Km = (500-0.1*500) / (0.1*0.005) = 4 500 000/5 = 9*105 Н*м
3) Сдвиговая контактная жесткость полумуфт определяет величину упругого относительного смещения полумуфт без проскальзывания. Эта величина определяется в ходе проектного расчета нажимных элементов после определения их геометрии. Предварительно принимаем сдвиговую контактную жесткость полумуфт такой же, как и крутильную жесткость редуктора
Ks = 1 * 109 Н*м/рад.
4) Номинальный рабочий ход нажимного элемента уже назначен выше. При определении жесткости возвратных пружин мы задавались величиной хода 0.005 м.
5) Средний диаметр фрикционных элементов. Этот параметр совместно с усилием прижима и коэффициентом трения для фрикционных накладок определяет способность муфты передавать крутящий момент (передаваемый крутящий момент равен произведению среднего радиуса на усилие прижима и коэффициент трения). Задаваясь величиной коэффициента трения 0.2 и принимая номинальный передаваемый момент таким же, что и для редуктора (10 Н/м), получим средний диаметр фрикционных элементов Dср = 2 * 10 / (500-0.1*500) / 0.2 = 100 / 450 = 0.222м или, округляя с небольшим запасом, - 0.225 м.
6) Величиной коэффициента трения мы задавались при определении среднего диаметра фрикционных накладок – 0.2.
7) Момент инерции первой полумуфты. Часто эта полумуфта в подобных системах выполняется как маховик. Предположим, что рабочий ход наша машина совершает за половину времени цикла (0.5 с). Работа двигателя за это время составит 125/2 = 62.5 Дж. Чтобы избежать принудительной остановки машины, остальную часть энергии в систему должен отдать маховик. Исходя из характеристики двигателя (он имеет максимум мощности при угловой скорости 25 рад/с), желательно, чтобы угловая скорость маховика не падала ниже величины 20 рад/с. Если считать, что к началу рабочего хода двигатель успеет разогнать маховик до 30 рад/с, то момент инерции маховика, ориентировочно:
Jm1 = 2.*62.5 /(30-20)**2 = 1.25 кг*м2.
8) Момент инерции второй полумуфты принимаем соизмеримым с моментом инерции ведомого колеса редуктора – 0.1 кг*м2.
9) Масса нажимного элемента будет определена в ходе конструктивной проработки муфты. Зададимся пока величиной 1 кг.
FTR – источник импульса силы трапециевидной формы. Параметры этого двухполюсника, моделирующего усилие прижима, берем из графика "Изменение усилия прижима дисков сцепления муфты" на рис. 5.1:
1) Начальный уровень силы – 0 Н
2) Максимальное значение силы – 500 Н
3) Момент начала изменения усилия – 6 с
4) Продолжительность начального участка изменения силы – 0.3 с
5) Продолжительность пологого участка с постоянным значением силы – 1000с (взяли с запасом).
6) Продолжительность конечного участка изменения силы – 0 (параметр не важен для нашего случая).
K – осевой идеально упругий элемент. В нашей модели используется в двух местах. Величину крутильной жесткости можно будет определить, назначив в ходе проектирования размеры двух участков вала. Сейчас, ориентировочно, принимаем жесткость обоих участков вала 1*109 Н*м/рад, как и жесткость редуктора.
Теперь соединим выбранные модели элементов и пронумеруем полученные степени свободы объекта. Исходя из вышеизложенного, в формируемом фрагменте привода используется четыре двухполюсника (DVL,K,REDCT,FTR) и один трехполюсник (MUFTA). Соединение этих элементов и нумерация глобальных степеней свободы, предлагаемая авторами, изображена на рис.5.3. Степени свободы фрагмента кратко перечислены ниже:
1 – связана с опорой привода;
2 – поворот вала двигателя;
3 – поворот ведущих частей муфты;
4 – поворот ведомых частей муфты;
5 – перемещение нажимного элемента муфты;
6 – поворот ведущей шестерни редуктора;
7 – поворот выходного вала редуктора.
Из выделенных степеней свободы две являются внешними (они соединяются со степенями свободы других фрагментов). В нашем случае при описании общей модели объекта фрагмент привода будет соединен с фрагментом исполнительного механизма по степеням свободы, соответствующим опоре и углу поворота выходного вала редуктора.
Для отладки работы фрагмента и последующего вывода данных, необходимых для проектного расчета, определим список выходных переменных и имена программ расчета выходных переменных, которые будут использованы для этого:
- моменты на участках вала, на входном и выходном валах редуктора (программа X);
- потери в муфте (программа DIS);
- усилие прижима дисков муфты, усилие на толкателе возвратных пружинах муфты (программа X);
- угловая скорость вала двигателя и ведомых частей муфты (программа V).
|
|
|
|
Рис. 5.3. |
Декомпозиция на элементы фрагменты привода и нумерация степеней свободы его математической модели. |
Параметры, необходимые для программ расчета выходных переменных X и V, остались у нас в памяти со времени написания (изучения) предыдущего раздела. Для этих программ необходимо задать указатель на соответствующую внутреннюю переменную и масштаб вывода. С программой DIS мы еще не встречались, поэтому:
> ARM ? DIS
DIS – программа расчета потерь энергии в двухузловом элементе. Для этой программы необходимо задать следующие указатели:
1 – номер степени свободы, связанный с первой ветвью элемента;
2 – указатель на усилие, действующее по первой ветви элемента;
3 – номер степени свободы, связанный со второй ветвью элемента;
4 – указатель на усилие, действующее по второй ветви элемента.
Кроме того, для этой программы, как и для программ X и V, требуется задать масштаб вывода рассчитываемой величины.
Итак, предварительная работа по подготовке модели привода проделана, и мы можем написать задание для анализа автономной работы привода. Попутно изучим еще одну возможность, часто используемую в разделах описания данных – составные списки параметров.
Как уже говорилось выше, можно раздел DATA нашего описания задания определить в таком виде:
$ DATA :
Параметры двигателя = 10, 50, 0, 1000, 2.5 E-3, 1;
Параметры муфты = 1E4, 9E5, 1E9, 5E-3, 0.225,
0.2, 1.25, 0.1, 1
Параметры редуктора =4,0.96,10,1.E9,0.005,0.08;
Усилие прижима=0,500,6,0.3,1000,0;
Жесткость вала 1 = 1E9; Жесткость вала 2 = 1E9;
Масштаб сил = 1; Масштаб моментов = 1;
Масштаб перемещений и скоростей = 1;
Масштаб работы = 1
Этот раздел описания данных отличается от раздела описания данных предыдущей задачи тем, что списки параметров для используемых здесь моделей элементов состоят не из одного, а из несколько параметров. Читаемость такого текста резко ухудшается и затруднена замена параметров (трудно вспомнить, какая цифра какому именно параметру соответствует). Поэтому, в нашей программе этот раздел будет выглядеть по-другому:
$ DATA :
{ Двигатель }
Пусковой момент двигателя = 10;
Скорость холостого хода = 50;
Время включения = 0;
Время выключения = 1000;
Момент инерции ротора = 2.5 E-3;
Момент инерции корпуса = 1 ;
Параметры двигателя = Пусковой момент двигателя,
Скорость холостого хода,
Время включения, Время выключения,
Момент инерции ротора,
Момент инерции корпуса;
{ Муфта }
Жесткость возвратных пружин = 1. E4
Осевая жесткость полумуфт = 9. E5
Сдвиговая жесткость полумуфт = 1. E9
Рабочий ход нажимного элемента = 0.005
Средний диаметр дисков трения = 0.225
Коэффициент трения = 0.2
Момент инерции первой полумуфты = 1.25
Момент инерции второй полумуфты = 0.10
Масса нажимного элемента = 1
Параметры муфты = Жесткость возвратных пружин,
Осевая жесткость полумуфт,
Сдвиговая жесткость полумуфт,
Рабочий ход нажимного элемента,
Средний диаметр дисков трения,
Коэффициент трения,
Момент инерции первой полумуфты,
Момент инерции второй полумуфты,
Масса нажимного элемента;
{ Редуктор }
Передаточное отношение = 4;
К. п. д. = 0.96;
Номинальный момент = 10;
Жесткость передачи = 1 E9;
Момент инерции шестерни = 0.005;
Момент инерции колеса = 0.08;
Параметры редуктора = Передаточное отношение,
К. п. д.,
Номинальный момент,
Жесткость передачи,
Момент инерции шестерни,
Момент инерции колеса;
{ Управление муфтой }
Начальное усилие прижима = 0
Максимальное усилие прижима = 500
Начало включения муфты = 6
Продолжительность роста усилия = 0.3
Время работы муфты = 1000
Продолжительность спада усилия = 0
Усилие прижима = Начальное усилие прижима,
Максимальное усилие прижима,
Начало включения муфты,
Продолжительность роста усилия,
Время работы муфты,
Продолжительность спада усилия;
{ Участки вала }
Жесткость участка вала 1 = 1 E9
Жесткость участка вала 2 = 1 E9
{ Масштабы рассчитываемых выходных
переменных }
Масштаб сил = 1
Масштаб моментов = 1
Масштаб перемещений и скоростей = 1;
Масштаб работы = 1
Как видно из приведенного примера, использование составных списков параметров, особенно если не пожалеть времени на вразумительные идентификаторы и комментарии, резко улучшает читаемость получаемой программы и упрощает дальнейшую работу с ней. Следующий этап формирования задания – раздел FRAGMENT:
$ FRAGMENT : Привод
# BASE : 1
# STRUCT :
Двигатель 'DVLT (2 1; Параметры двигателя)
Участок вала N1 'K (2 3; Жесткость участка вала 1)
Муфта включения 'MUFTA (3 4 5; Параметры муфты)
Участок вала N2 'K (4 6; Жесткость участка вала 2)
Редуктор 'REDCT (6 7; Параметры редуктора)
Управляющий элемент'FTR (5 1; Усилие прижима)
# OUTPUT :
Момент на первом валу 'X (I: Участок вала N1;
Масштаб моментов )
Момент на втором валу 'X (I: Участок вала N2;
Масштаб моментов )
Момент на входе редуктора 'X (I: Редуктор ;
Масштаб моментов)
Момент на выходе редуктора 'X (I: Редуктор (2);
Масштаб моментов)
Потери в муфте 'DIS (3, I: Муфта включения (1),
4, I: Муфта включения (2);
Масштаб работы)
Усилие прижима дисков муфты 'X (W: Муфта включения (1);
Масштаб сил)
Усилие возвратных пружин муфты 'X (W: Муфта включения (2);
Масштаб сил)
Усилие на толкателе муфты 'X (I: Муфта включения (3);
Масштаб сил)
Угл. ск. вала двигателя 'V (2;
Масштаб перемещений и скоростей)
Угл. ск. ведом. частей муфты 'V (4;
Масштаб перемещений и скоростей)
# EXTERNAL : 1, { система отсчета}
7 { выходной вал редуктора }
И, наконец, разделы описания задания. По ходу расчета есть смысл контролировать три величины – угловая скорость ведущих и ведомых частей муфты (должны изменяться в интервале 0-50 рад/с), усилие прижима дисков муфты (0 – 1000). Отображение результатов по окончании расчета удобно задать, используя возможности автоматического масштабирования. Тогда текст задания на расчет и отображение результатов будет выглядеть следующим образом:
$ RUN :
Автономная работа привода ' SHTERM (END=10;
Угл. ск. вала двигателя = (0, 50),
Угл. ск. ведом. частей муфты = (0, 50),
Усилие прижима дисков муфты = (0, 1000)
)
$ PRINT :
Работа муфты привода ' DISP (;
Угл. ск. вала двигателя ,
Угл. ск. ведом. частей муфты ,
Усилие на толкателе муфты ,
Усилие возвратных пружин муфты,
Усилие прижима дисков муфты )
Работа трения в муфте ' DISP (;
Момент на входе редуктора ,
Момент на выходе редуктора,
Момент на первом валу,
Момент на втором валу, Потери в муфте)
$ END
Запишем полученную программу на языке PRADIS в файл TEST5P. Так же, как и раньше, выполним анализ полученной модели:
> SLANG TEST5P
5.3.2. Анализ результатов моделирования привода и некоторые возможности управления программой интегрирования
Анализируемый процесс не отличается особой сложностью, и мы можем без труда разобраться в событиях, изображенных на экране. В начальный момент времени включается двигатель, и угловая скорость вала двигателя начинает возрастать. Через 6 секунд после включения двигателя (в момент включения муфты) угловая скорость вала двигателя несколько превосходит 30 рад/с. Включение муфты характеризуется на экране ростом усилия на толкателе муфты. Вначале это усилие идет на преодоление сопротивления возвратных пружин, а после смыкания фрикционных дисков – и на создание усилия прижима этих дисков друг к другу. В результате этого между фрикционными дисками появляется момент трения, который приводит к росту угловой скорости ведомых частей муфты и падению оборотов вала двигателя (ведущих частей муфты). После смыкания фрикционных дисков продолжается совместный разгон ведущих и ведомых частей муфты.
Но если говорить об общем впечатлении, полученном авторами на своем компьютере от процесса интегрирования, то его нельзя трактовать как восторг. Скорее – легкое разочарование. По своей сути задача проста. И если даже она решается так медленно, то что будет с более сложными задачами?
Естественно, что комплекс PRADIS, разрекламированный ранее как весьма подходящий для столяра инструмент, должен иметь хотя бы минимальные средства (например, шенкеля), позволяющие некоторым наиболее одаренным пользователям ставить его на дыбы, переводить из неспешной рыси в галоп и, при удачном стечении обстоятельств, даже сокращать время, проводимое ежедневно за экраном в ожидании конца забега.
В этом подразделе мы намеревались несколько приоткрыть цветастую попону, прикрывающую бока программы интегрирования, этой рабочей лошади инженера-расчетчика, и показать на ее рельефном мускулистом теле точки, куда можно вонзать шпоры. Естественно, что наиболее опасные из них будут изучаться позже, когда нога пользователя уже будет хорошо чувствовать лошадь. А сейчас мы посмотрим наиболее безопасные, которые, в самом худшем случае, могут заставить ее пританцовывать на месте, но ни в коем случае не приведут к падению в грязь.
Следует обратить внимание на следующий момент. Настройка программы интегрирования для различных установок комплекса может изменяться. В этом документе, когда речь идет о статистике результатов расчетов, приводятся результаты, полученные авторами на имеющемся у них экземпляре комплекса. У каждого конкретного пользователя статистика может отличаться от тех результатов, что приводятся в этом документе. Поэтому для пользователя есть прямой смысл проводить численные эксперименты и анализ результатов параллельно, сравнивая их с теми, что приводятся в этом документе.
Вкратце программа интегрирования действует по следующему алгоритму. Интегрирование начинается с минимального шага, который, как правило, заведомо мал. Сделав два-три мелких начальных шага, программа интегрирования на каждом последующем шаге оценивает текущую погрешность интегрирования. Если ПОЛУЧЕННАЯ НА ОЧЕРЕДНОМ ШАГЕ погрешность интегрирования (или еще говорят ЛОКАЛЬНАЯ погрешность интегрирования) меньше допустимой погрешности, то делается попытка увеличить шаг интегрирования. Однако, если очередной шаг станет очень большим (по сравнению с длительностью определяющих поведение системы процессов), то до оценки локальной погрешности дело может не дойти. Это будет в том случае, если на шаге интегрирования не будет обеспечена сходимость процесса решения системы нелинейных алгебраических уравнений. Тогда будет сделана попытка уменьшить шаг интегрирования. При этом шаг будет дробиться до тех пор, пока не будет обеспечено достижение сходимости решения системы нелинейных алгебраических уравнений. Для того, чтобы шаг интегрирования не был слишком большим, и программа не попадала часто в область несходимости, его ограничивают некоторой предельной величиной. По умолчанию величина предельного шага интегрирования обычно 0.01 с., но может быть изменена пользователем.
Увеличим предельный шаг интегрирования. За величину предельного шага отвечает ключевой параметр программы интегрирования SMAX. Зададим величину предельного шага интегрирования равной 0.02 с, внеся соответствующие изменения в раздел RUN:
$ RUN :
Автономная работа привода ' SHTERM (END=10, SMAX=0.02;
Угл. ск. вала двигателя = (0, 50),
Угл. ск. ведом. частей муфты = (0, 50),
Усилие на толкателе муфты = (0, 1000),
Усилие прижима дисков муфты = (0, 1000),
Усилие возвратных пружин муфты = (0, 1000)
)
Будем удваивать предельный шаг интегрирования, сводя результаты в таблицу 5.1.
Таблица 5.1. Зависимость вычислительных затрат от ключевого параметра программы интегрирования SMAX
|
N |
SMAX |
Успешных шагов |
Потери шагов |
Всего итераций |
Время счета(с) |
Итераций на шаг |
|
1 |
0.01 |
1039 |
9/18 |
2198 |
204 |
2.008 |
|
2 |
0.02 |
548 |
13/20 |
1232 |
114 |
2.013 |
|
3 |
0.04 |
304 |
10/21 |
743 |
68 |
2.023 |
|
4 |
0.08 |
183 |
8/22 |
512 |
45 |
2.087 |
|
5 |
0.15 |
135 |
10/25 |
436 |
37 |
2.126 |
|
6 |
0.30 |
103 |
16/22 |
378 |
31 |
2.106 |
|
7 |
0.60 |
105 |
22/27 |
436 |
34 |
2.124 |
Как видно из приведенных в таблице данных, увеличение максимального шага интегрирования с величины 0.3 до величины 0.6 с привело к некоторому ухудшению результатов (количество итераций возросло, увеличилось и процессорное время работы программы интегрирования). При этом на этапе разгона ведущих частей привода шаг интегрирования уже не возрастал до предельной величины, а определялся в основном локальной погрешностью. Для данной задачи оптимальная величина предельного шага интегрирования, видимо, 0.3 с.
Предельный шаг интегрирования – это одна из величин, которые достаточно сильно влияют на продолжительность расчета. Его величину следует по возможности согласовывать с параметром END. В рассмотренной нами задаче неверное задание предельного шага интегрирования привело к возрастанию времени счета более чем в 6 раз.
5.3.3. Модель исполнительного механизма.
Результаты разбиения фрагмента рычажного механизма на элементы представлены на рис. 5.5. Список выделенных элементов выглядит следующим образом.
- основание, служащее для закрепления механизма;
- балочный упругий элемент, моделирующий кривошип (BALKA, Кривошип);
- стержневой упругий элемент (STRGN; Коромысло, Шатун);
- треугольный упругий элемент (TRGUL; Рычаг);
- точечный инерционный элемент (M; Ползун).
|
|
|
|
Рис. 5.5. |
Декомпозиция фрагмента рычажного механизма на элементы и нумерация степеней свободы его математической модели. |
В отличие от всех предыдущих фрагментов, этот фрагмент не имеет своих силовых элементов, задающих движение. Однако, для автономного тестирования фрагмента нужно, чтобы он воспроизводил какое-либо движение реального исполнительного механизма. Для этого можно было бы учесть силу тяжести ползуна, которая заставит переместиться механизм из начального положения в какое-то положение, соответствующее минимуму потенциальной энергии. Поэтому в тестовом расчете будет присутствовать еще элемент "Сила тяжести ползуна" (F).
Справка по включаемым в модель элементам говорит о том, что в качестве параметров для элементов BALKA, STRGN и TRGUL задаются координаты начального положения элементов и параметры материала, из которого они сделаны. Следуя принципу задания параметров для предварительного расчета, изложенному в подразделе 5.2, все параметры элементов, кроме начального значения координат, будем задавать ориентировочно. Предположим, что все рычаги механизма изготовлены из стали, масса каждого рычага 1 кг, центры тяжести стержневых элементов находятся в центре элемента, геометрический момент инерции кривошипа на изгиб – 1.E-6 м3, площадь поперечного сечения балочного и стержневых элементов – 1.E-4 м2, толщина треугольника = 0.01м. Зададимся массой ползуна 5 кг.
Разделы описания данных и описания объекта для этого фрагмента могут быть такими:
$ DATA :
{ Координаты начальных точек звеньев механизма}
Точка O = 0., 0. ;
Точка A = -0.134, 0.238;
Точка B = 0.173, -0.109;
Точка C = 0.092, -0.339;
Точка D = 0.55, -0.95 ;
Точка E = 0.55, 0.
{ Параметры материалов }
Модуль Юнга = 2. E11
Плотность = 7800
Коэффициент Пуассона = 0.3
{ Инерционные параметры - масса, положение центра тяжести}
Масса кривошипа = 1, 0.5
Масса коромысла = 1, 0.5
Масса шатуна = 1, 0.5
Масса ползуна = 5
{ Геометрические параметры сечений }
J кривошипа = 1.E-6
F кривошипа = 1.E-4
F коромысла = 1.E-4
F шатуна = 1.E-4
T рычага = 0.01
Сила тяжести ползуна = - 50. {Направлена вниз}
{ Масштабы вывода }
Масштаб вывода угла = 57.29 {угол - в градусах}
Масштаб вывода перемещения = 1 {перемещение - в метрах}
$ FRAGMENT: МЕХАНИЗМ
# BASE : 1,2, {опора кривошипа}
9,10, {опора коромысла}
13 {направляющая ползуна}
# STRUCT :
Кривошип 'BALKA (1 2 3 4 5 6;Точка O, Точка A,
Масса кривошипа,
J кривошипа,F кривошипа,
Модуль Юнга)
Коромысло'STRGN (9 10 7 8; Точка B, Точка E,
Масса коромысла,
F коромысла,Модуль Юнга)
Шатун 'STRGN (11 12 13 14; Точка C, Точка D,
Масса шатуна,
F шатуна, Модуль Юнга)
Рычаг 'TRGUL (4 5 7 8 11 12;Точка A, Точка B, Точка C,
T рычага, Модуль Юнга,
Коэффициент Пуассона,
Плотность)
Ползун 'M (14; Масса ползуна)
Сила тяжести 'F (14; Сила тяжести ползуна)
# EXTERNAL : 1, {опора }
3, {вращение кривошипа}
14 {вертикальное перемещение ползуна}
Выходные переменные, которые понадобятся нам для определения нагрузок на элементы, определим после автономной отладки этого фрагмента. А сейчас нужно будет задать вывод, который позволит нам проконтролировать правильность сборки модели. Как показывает опыт, для плоских и пространственных механизмов контроль правильности сборки модели имеет особую актуальность. Однако проконтролировать правильность работы механизма, используя только графики или числовой вывод перемещений характерных точек, в короткие сроки практически невозможно. Поэтому для контроля правильности сборки механизма будем использовать другое средство комплекса – изображение объекта в ходе расчета. А в подразделе OUTPUT формируемого нами задания определим вывод двух величин – угла поворота кривошипа и вертикального перемещения ползуна:
# OUTPUT :
Угол поворота кривошипа 'S ( 3; Масштаб вывода угла)
Перемещение ползуна 'S (14; Масштаб вывода перемещения)
5.3.4. Изображение объекта – раздел SHOW.
Для изображения объекта на экране после расчета необходимо включить в текст программы раздел SHOW. Этот раздел в программе всегда один и следует за разделом FRAGMENT (если этих разделов несколько – то за последним из них. В этом случае в разделе SHOW формируется изображение объекта, определенного в этом фрагменте).
Раздел SHOW состоит из описания одного или нескольких слоев изображения. Состав слоя изображения может быть самым разнообразным и включать в себя как изображение всего объекта, так и его отдельных частей. Каждый слой характеризуется своим масштабом изображения, своей точкой зрения наблюдателя и своим цветом.
|
|
|
|
Рис. 5.6. |
Иллюстрация к принципам позиционирования изображения на экране. |
В этом пункте руководства мы познакомимся с простейшей возможностью изображения объекта на экране в ходе расчета – изображением объекта "по умолчанию". Использование этой возможности предполагает, что в формируемое изображение будут включены графические образы тех элементов объекта, для которых определены графические образы элементов "по умолчанию". В нашем случае в формируемое изображение будут включены графические образы кривошипа, коромысла, шатуна и рычага, что вполне достаточно для контроля правильности сборки механизма. При этом все изображение будет включено в один слой.
Очевидно, первое, что нам нужно сделать при формировании изображения, – это определить его масштаб, цвет и задать точку зрения наблюдателя.
Принципы масштабирования изображения и определения точки зрения наблюдателя для каждого слоя показаны на рис. 5.6 и 5.7.
Наблюдатель видит объект через трубку прямоугольного сечения (рис.5.6a). Предполагается, что изображение объекта не искажается (т.е., масштабируется одинаково по всем осям пространства). Прямоугольное окно экрана дисплея, на котором будет размещаться изображение, геометрически подобно сечению трубки.
Поэтому для определения размера ее поперечного сечения достаточно задать только один размер, в данном случае, размер меньшей стороны сечения (= размер вписанной в сечение окружности).
Для определения положения трубки в пространстве задаются координаты следующих точек:
1) Точка C. Лежит на оси трубки и определяет центр связанной с ней системы координат X', Y', Z'.
2) Точка A. Лежит на оси трубки (Z') и совместно с точкой C определяет ее направление в пространстве.
3) Точка B. Определяет положение плоскости, проходящей через оси Z' и X'. Заметим, что точка B' не обязательно должна лежать непосредственно на оси X', поскольку иногда бывает затруднительно определить координаты точек A, C и B так, чтобы между осями X' и Z' выдерживался прямой угол.
Вооруженный трубой наблюдатель видит объект в проекции, перпендикулярной оси трубы (рис. 5.6б). Получаемое изображение будет соответствовать случаю, когда пользователь смотрит из точки A в точку C. На состав изображения не влияет, находится ли часть объекта за предполагаемым положением наблюдателя или перед ним – весь объект проецируется на плоскость, определяемую прямыми X' и Y'. Для размещения этого изображения на экране дисплея в прямоугольном поле изображения объекта руководствуются следующими простыми правилами (рис. 5.7):
1) Центр трубки (т.C) помещается в центр изображения объекта.
2) Ось X' связанной с трубой системы координат располагается горизонтально (от точки C вправо), ось Y' – вертикально (от точки C – вверх), ось Z' – перпендикулярно плоскости экрана (от точки C на наблюдателя).
3) Поперечное сечение трубки точно вписывается в границы поля изображения объекта. Поэтому нужное масштабирование изображения (т.е. размер изображения на экране) достигается выбором соответствующего значения диаметра вписанной в сечение окружности (чем БОЛЬШЕ диаметр, тем МЕНЬШЕ изображение).
|
|
|
|
Рис. 5.7. |
Экран дисплея в режиме изображения объекта и схема определения точки зрения наблюдателя.
|
При изображении плоских объектов удобно задавать для точек A и B нулевые координаты. Тогда предполагается, что поле изображения объекта будет лежать в плоскости XOY, а его границы будут параллельны осям OY и OX (т.е., поле изображения объекта будет находиться в таком положении, как это изображено на рис. 5.7).
Таким образом, список параметров, задаваемых для каждого слоя изображения, включает в себя:
· размер меньшей стороны прямоугольного сечения трубки;
· пространственные координаты центра трубки (точки C);
· пространственные координаты точки A;
· пространственные координаты точки B;
· номер цвета слоя.
Относительно выбора номера цвета слоя поговорим в следующей главе. Пока можно задавать нулевое значение номера цвета (определять выбор цвета по умолчанию).
В нашем случае, поскольку предполагается изображение плоского объекта, можно предложить следующие параметры слоя:
Диаметр окружности = 2.0
Центр экрана = 0, -0.7, 0 {X, Y, Z}
Вспомогательные точки = 0,0,0, 0,0,0
Цвет изображения = 0 {По умолчанию}
Эти списки параметров внесем в раздел DATA формируемого нами задания. А после раздела FRAGMENT в текст задания включим раздел SHOW с описанием единственного слоя изображения "по умолчанию":
$ SHOW
Изображение механизма 'LAYER (; Диаметр окружности,
Центр экрана,
Вспомогательные точки,
Цвет изображения)
Разделы RUN и PRINT пусть будут пока простейшими:
$ RUN :
Автономный анализ механизма 'SHTERM (END=2, SMAX=0.1)
$ PRINT :
Результаты расчета ' DISP ()
$ END
Запишем сформированное нами задание в файл TEST5M и выполним для него команду SLANG.
Судя по изображению на экране, в описании объекта допущена ошибка. В своем начальном положении механизм похож на то, что мы ожидали увидеть, но после небольшого поворота коромысло отрывается и начинает жить своей, не зависимой от остального механизма жизнью.
Обнаруженная выше ошибка может быть вызвана:
а) неверным описанием связей (коромысло соединили не с теми узлами модели);
б) неверным описанием координат коромысла. Хотя, в данном случае, это вряд ли, как говорил товарищ Сухов – если бы была ошибка в определении координат, то уже в начальном положении коромысло было бы оторванным;
в) несогласованное задание координат и степеней свободы для коромысла.
Внимательное рассмотрение текста описания объекта показывает, что при описании коромысла первыми указаны степени свободы, соответствующие точке E, а в списке параметров для этого элемента – координаты точки B. Исправим эту ошибку (в списке параметров поменяем местами координаты точек). Наиболее любознательные из пользователей могут проверить, что это и было причиной странного поведения механизма.
5.3.5. Сборка модели технологической машины из отлаженных фрагментов.
ПРИМЕЧАНИЕ. ЗАРАНЕЕ ПРИНОСИМ ПОЛЬЗОВАТЕЛЮ СВОИ ИЗВИНЕНИЯ ЗА НЕКОТОРОЕ СТИЛИСТИЧЕСКОЕ НЕСОВЕРШЕНСТВО ЭТОГО ПУНКТА, ПОСКОЛЬКУ ОН БЫЛ НАПИСАН В ПЕРИОД ШТУРМА БЕЛОГО ДОМА ПРЕЗИДЕНТСКИМИ ВОЙСКАМИ.
Следующей задачей, стоящей перед нами, является сборка модели технологической машины рис. 5.1.
На этот раз текст задания будет состоять из нескольких фрагментов. Это – фрагменты ПРИВОД и МЕХАНИЗМ, отлаженные в предыдущих разделах этой главы, а также текст глобального фрагмента, описывающего структуру машины в целом. Как уже было сказано, в тексте описания глобального фрагмента можно использовать фрагменты ПРИВОД и МЕХАНИЗМ как "макроэлементы".
"Декомпозиция" глобального фрагмента на элементы изображена на рис. 5.8. В простейшем случае фрагменты, отлаженные ранее, можно использовать с теми параметрами, которые были заданы при их описании. Для каждого из ранее определенных фрагментов должны быть заданы степени свободы, которые служат для соединения этих фрагментов с остальной системой. Эти степени свободы описываются в подразделах EXTERNAL (см. тексты описания фрагментов в пунктах 5.3.1 и 5.3.3). Раньше о подразделе EXTERNAL ничего не говорилось, а этот подраздел включался в текст описания объекта без каких-либо комментариев. Его назначение – описать узлы фрагмента, служащие для соединения с другими фрагментами и элементами системы.
|
|
|
|
Рис. 5.8. |
Связи между элементами и нумерация степеней свободы математической модели машины. |
В каждом новом фрагменте, в том числе в тексте глобального фрагмента, нумерация узлов является независимой. Все номера узлов фактически являются внутренними для текущего фрагмента и никак не влияют на нумерацию узлов других фрагментов. Но, чтобы эта независимость фрагмента не перерастала в его игнорирование со стороны системы, его связь с другими элементами объекта нужно как-то определить и описать. Для этого в подразделе EXTERNAL перечисляются номера узлов, которые служат для его включения в описание глобального фрагмента. В тексте глобального фрагмента каждый из включаемых в него фрагментов будет иметь столько степеней свободы, сколько их описано в подразделе EXTERNAL включаемого фрагмента. Порядок описания узлов при включении фрагмента должен соответствовать порядку их описания в подзаголовке EXTERNAL.
При описании закрепления фрагмента и его внешних узлов следует иметь в виду следующую особенность алгоритма формирования системы уравнений комплекса PRADIS. Для формирования системы уравнений осуществляется перенумерация степеней свободы объекта. Это делается потому, что номера узлов, задаваемые пользователем, не обязательно являются последовательными целыми числами (они могут содержать пропуски). После перенумерации этот возможный недостаток устраняется. Кроме того, для сокращения вычислительных затрат, при перенумерации всем закрепленным узлам фрагмента присваивается один и тот же номер. Для них формируется одно уравнение (уравнение равновесия для тела, связанного с системой отсчета). Если этот фрагмент является глобальным, то это уравнение не анализируется (фактически вычеркивается из результирующей системы уравнений), и все степени свободы, описанные в подзаголовке #BASE, считаются неподвижными.
Ситуация изменяется, когда ранее описанный фрагмент используется в качестве макроэлемента. Если ни один из закрепленных узлов включаемого фрагмента не описан в подразделе EXTERNAL (и, следовательно, не может быть связан с закрепленным узлом глобального фрагмента), то, как и все остальные узлы этого фрагмента, при перенумерации он получает соответствующий уникальный номер и становится незакрепленным. Этот номер для всех базовых узлов включаемого фрагмента будет одинаковым. Если хотя бы один из базовых узлов является внешним, то все базовые узлы включаемого фрагмента при перенумерации получают тот же номер, что и соответствующие им узлы глобального фрагмента. Для того, чтобы сохранить прежнее закрепление включаемого фрагмента, нужно один базовый узел этого фрагмента описать в качестве внешнего и при включении связать его с базовым узлом глобального фрагмента. Поскольку все закрепленные узлы фрагмента – это фактически один и тот же узел, то в подразделе EXTERNAL запрещается описывать более одного закрепленного узла.
Заметим, что фрагмент МЕХАНИЗМ имеет пять закрепленных узлов (1,2,9,10,13), однако, в соответствии с вышесказанным, только один из них (1) описан в качестве внешнего. В случае, если при описании включения фрагмента МЕХАНИЗМ этот узел будет связан с базовым узлом глобального фрагмента (как мы и намерены сделать), то этого окажется достаточно, чтобы сохранить прежнее закрепление.
Вернемся к формированию текста глобального фрагмента. Из новых элементов для его описания нам понадобится только элемент UPRP (справка по элементу – ARM ? UPRP). Этот элемент имеет две степени свободы. Для него задаются три параметра – начальная величина зазора, величина коэффициента жесткости упругого участка нагрузки и максимальная величина силы, соответствующая участку с величиной силы, не зависящей от перемещения.
Структура описания объекта в случае использования нескольких фрагментов будет несколько отличаться от структуры рассмотренных ранее программ. Все данные для каждого из фрагментов могут быть объединены в единый раздел описания данных. После раздела описания данных в тексте описания объекта должны присутствовать разделы FRAGMENT с описанием каждого из фрагментов ПРИВОД и МЕХАНИЗМ. Порядок следования этих фрагментов в тексте задания не существенен. Последним в тексте описания объекта должен присутствовать текст описания глобального фрагмента, т.е. того фрагмента, который в конечном итоге будет подвергаться анализу. Назовем для определенности глобальный фрагмент МАШИНА. Тогда, если перечислять порядок следования разделов описания объекта, в нашем случае он может быть следующим:
$ DATA :
$ FRAGMENT: ПРИВОД
$ FRAGMENT: МЕХАНИЗМ
$ FRAGMENT: МАШИНА
Оперировать с единым блоком данных не всегда удобно. В том виде, в котором до сих пор использовался раздел описания данных, он называется глобальным (непоименованным) разделом описания данных. Такой раздел включает в себя списки параметров, действительные для всей программы, и всегда находится в начале программы. Кроме этой возможности для каждого из фрагментов могут быть созданы локальные блоки данных, списки параметров в которых будут справедливы только для конкретного фрагмента. Раздел описания данных, содержащий локальный блок данных для фрагмента, является поименованным и в тексте программы следует всегда перед текстом соответствующего фрагмента. Одна из возможных последовательностей разделов описания объекта в случае использования локальных блоков данных:
$ DATA : {глобальный блок данных}
$ DATA : ПРИВОД {данные для фрагмента ПРИВОД}
$ DATA : МЕХАНИЗМ {данные для фрагмента МЕХАНИЗМ}
$ FRAGMENT: МЕХАНИЗМ
$ FRAGMENT: ПРИВОД
$ DATA : МАШИНА {данные для фрагмента МАШИНА}
$ FRAGMENT: МАШИНА
При любом способе описания объекта разделы описания данных и описания фрагмента МАШИНА имеют следующий вид:
$ DATA :
Зазор между ползуном и нагрузкой = 0.2
Жесткость упругого участка = 5000. (500/(0.3-0.2))
Максимальная сила = 500.
$ FRAGMENT : МАШИНА
# BASE : 2
# STRUCT :
Привод 'ПРИВОД (2 1)
Исполнительный механизм'МЕХАНИЗМ (2 1 3)
Нагрузка 'UPRP (2 3; Зазор между ползуном и нагрузкой,
Жесткость упругого участка,
Максимальная сила)
# OUTPUT:
Усилие технологической операции'X (I:Нагрузка; 1)
$ SHOW
Изображение механизма 'LAYER (; Диаметр окружности,
Центр экрана,
Вспомогательные точки,
Цвет изображения)
Раздел описания изображения объекта может пока оставаться неизменным (т.е., требовать изображения объекта по умолчанию).
В разделе описания задания удобно использовать два вызова программы интегрирования. Первый – для анализа процесса разгона маховика, второй – включение муфты и рабочий цикл машины (на самом деле в шестой главе мы вообще не будем анализировать процесс разгона маховика, а этот пример приводим здесь из педагогических соображений – чтобы показать как можно использовать несколько вызовов программы интегрирования для расчета нескольких стадий процесса). Переменные, отображаемые по результатам расчета в разделе PRINT, удобно группировать по признаку отношения к тому или иному элементу или узлу машины: например, данные, относящиеся к муфте, данные, относящиеся к рычагам и т.д.:
$ RUN :
Разгон маховика ' SHTERM (END=6, SMAX=0.3;
Привод/ Угл. ск. вала двигателя = (0, 50),
Привод/ Угл. ск. ведом. частей муфты = (0, 50))
Рабочий цикл ' SHTERM (END=2, SMAX=0.1;
Привод/ Угл. ск. вала двигателя = (0, 50),
Привод/ Угл. ск. ведом. частей муфты = (0, 50),
Исполнительный механизм/ Перемещение ползуна,
Исполнительный механизм/ Угол поворота кривошипа,
Усилие технологической нагрузки = (-500, 500))
$ PRINT :
Работа муфты привода ' DISP (;
Привод/Угл. ск. вала двигателя ,
Привод/Угл. ск. ведом. частей муфты ,
Привод/Усилие на толкателе муфты ,
Привод/Усилие возвратных пружин муфты,
Привод/Усилие прижима дисков муфты )
Продольные усилия в рычагах' DISP (;
Исполнительный механизм/ Угол поворота кривошипа,
Исполнительный механизм/Продольное усилие в шатуне,
Исполнительный механизм/Продольное усилие в коромысле)
$ END
Естественно, что при таком выводе раздел #OUTPUT фрагмента МЕХАНИЗМ должен быть дополнен описанием выходных переменных "Продольное усилие в шатуне" и "Продольное усилие в коромысле".
В приведенном тексте можно заметить еще одну особенность заданий, содержащих несколько фрагментов. Для отображения выходной переменной необходимо указывать ее полный идентификатор, состоящий из последовательности идентификаторов входящих друг в друга фрагментов и собственного идентификатора выходной переменной, разделенные символом "/". Обратите внимание, что нужно указать не имя фрагмента (фрагментов с одинаковым именем во фрагменте более высокого уровня может быть много), а его идентификатор. Применительно к нашему заданию, имя фрагмента, моделирующего привод – ПРИВОД, а его идентификатор – Привод. Продолжая разговор на эту тему, предположим, что необходимо вывести выходную переменную XXX, непосредственно описанную во фрагменте с идентификатором YYY, который содержится во фрагменте ZZZ, входящем в глобальный фрагмент. Тогда полный идентификатор указанной выходной переменной будет:
ZZZ / YYY / XXX
5.3.6. Использование инструкции препроцессора $INCLUDE.
Если теперь попытаться получить единый текст описания модели технологической машины, включающий фрагменты привода и механизма, а также все блоки данных, то получим файл значительных размеров. Работать с ним будет сложно и неудобно. Поэтому, в таких случаях часто пользуются инструкцией препроцессора $INCLUDE. Она позволяет включать в текст программы на языке PRADIS содержимое других файлов. При этом текст включаемого файла помещается в текст обрабатываемой программы непосредственно в том месте, где находится инструкция $INCLUDE.
Вернемся к разбираемому примеру. Допустим, блок данных и фрагмент привода находятся в файле PRIVOD, блок данных и фрагмент исполнительного механизма – в файле MEHAN, а описание изображения объекта в ходе расчета – в файле VISUAL. Тогда текст программы, описывающей всю машину, мог бы выглядеть так (без учета инструкций описания задания на расчет и отображение):
$ DATA :
Зазор между ползуном и нагрузкой = 0.2
Жесткость упругого участка = 5000. {500/(0.3-0.2)}
Максимальная сила = 500.
$ INCLUDE : PRIVOD { описание привода}
$ INCLUDE : MEHAN { описание механизма}
$ FRAGMENT : МАШИНА
# BASE : 2
# STRUCT :
Привод 'ПРИВОД (2 1)
Исполнительный механизм'МЕХАНИЗМ (2 1 3)
Нагрузка 'UPRP (2 3; Зазор между ползуном и нагрузкой,
Жесткость упругого участка,
Максимальная сила)
# OUTPUT:
Усилие технологической нагрузки'X (I:Нагрузка; 1)
$ INCLUDE : VISUAL { описание изображения}
В данном случае использование инструкции $INCLUDE позволило структурировать информацию. Естественно, что в этом примере файлы PRIVOD и MEHAN должны содержать только разделы DATA и FRAGMENT (со своими именами, т.е., поименованные). Концовка программы (разделы PRINT, RUN и END) может находиться в этом файле, в файле VISUAL или быть выделенной в отдельный файл. В случае выделения разделов описания задания и заголовка END в отдельный файл его можно использовать как при анализе всего задания, так и в случае запуска задания для уже сформированной модели.
Нужно сказать, что включаемые файлы не обязательно должны содержать полностью законченные разделы программы. В этих файлах могут быть также какие-то участки полного текста раздела или даже участки отдельных списков параметров.
Приведем пример такого использования инструкции $INCLUDE. Для расчета динамики привода с кулачковым механизмом профиль кулачка задается таблицей "угол поворота кулачка – подъем толкателя". Подготовка такой таблицы может быть осуществлена автономной программой профилирования кулачка. Тогда, в разделе описания данных профиль кулачка можно описать так:
Профиль кулачка =
$ INCLUDE : COORD.DAT
В файле COORD.DAT в данном случае будут находиться данные по профилю кулачка, заданные, например, в таком виде:
. . .
10., 0.0898,
20., 0.875,
. . .
Таким образом, файл COORD.DAT легко может быть подготовлен в автоматизированном режиме, и его не обязательно включать в текст основной программы.
Вложенность инструкций $INCLUDE не ограничена. Т.е., включаемые файлы сами могут содержать инструкции $INCLUDE. Поэтому, нужно быть осторожным и не зациклить программу. Если файл A содержит требование включить в текст файл B, файл B – включить файл C, а файл C – включить файл A (хотя очень трудно представить себе такую ошибку для программы на языке PRADIS, скорее она может быть характерна для процедурных языков) – то, в зависимости от размеров свободного дискового пространства, вы можете очень долго ждать, когда препроцессор закончит свою работу. Как и всякое средство, использование возможности включения файлов в текст задания следует ограничить разумными пределами. Во многих программах естественной выглядит вложенность на один-три уровня. Однако, сомнительным представляется случай, когда вложенность достигает десяти уровней. Такая программа, конечно, будет обработана, но вероятность ошибки в ней, видимо, будет большой.
Когда вы будете решать вопрос о применении или неприменении в каждом конкретном случае этого средства, подумайте о пользователе, который будет использовать вашу модель. Если, для того, чтобы разобраться в тексте программы, он должен будет продираться через лес $INCLUDE, вряд ли он скажет вам спасибо.
Но, если вы хотите ему насолить, помните, что особенно эффектно включение вложенных инструкций $INCLUDE выглядит там и сям внутри сложного подраздела #STRUCTURE, особенно, если #OUTPUT ссылается на модели, описанные на шестом-седьмом уровне вложенности. Однако, применяя такие приемчики, рискуете однажды услышать сказанное приглушенно вам в спину: "Заставь дурака Богу молиться, ...".
В качестве упражнения, пользователь сам теперь может попробовать довести описание объекта до конца и выполнить задание на анализ всей машины в целом.
В следующей главе рассматриваются некоторые возможности изображения объекта в ходе анализа, позволяющие получить более эстетичную картинку. С учетом этого, будет предложен полный текст задания для моделирования машины, рассмотренной в этой главе. Используя этот текст, вместе с пользователем проведем несколько итераций по подбору параметров анализируемой машины по алгоритму, предложенному в разделе 5.2.
5.4. РЕЗЮМЕ.
1. Замена параметров в уже сформированной программе осуществляется с помощью раздела REPLACE. Все списки параметров, описанные в разделе REPLACE, замещают списки параметров в первоначальном тексте описания объекта.
2. При описании сложных фрагментов можно использовать возможности комплекса по фрагментации текста описания объекта. Тогда каждый из конструктивных узлов может описываться в виде отдельного фрагмента и отлаживаться отдельным заданием. В текст окончательного описания объекта такие фрагменты включаются как макроэлементы. Количество отдельных фрагментов (которые войдут затем в текст описания глобального фрагмента) не ограничивается.
3. В тексте глобального фрагмента каждый из включаемых в него фрагментов будет иметь столько степеней свободы, сколько их описано в подразделе EXTERNAL соответствующего фрагмента. При этом порядок описания узлов при включении фрагмента должен соответствовать порядку их описания в подразделе EXTERNAL.
4. В подразделе EXTERNAL может быть описано не более одного базового узла. Кроме того, в списке внешних узлов один и тот же узел не должен повторяться дважды или большее количество раз.
5. Полный идентификатор выходной переменной, входящей во включаемый фрагмент, содержит идентификатор этого фрагмента и идентификатор переменной, разделенные символом "/". Если переменная "спрятана" более глубоко, необходимо указывать "полный путь" к этой переменной – последовательность идентификаторов фрагментов, содержащих фрагмент с описанием требуемой выходной переменной. Раньше указывается идентификатор фрагмента более высокого уровня, последним – идентификатор переменной. Например, ZZZ / YYY / XXX (ZZZ – идентификатор фрагмента, входящего в глобальный фрагмент, YYY – идентификатор фрагмента, входящего в ZZZ, XXX – идентификатор выходной переменной, описанной в YYY).
6. В этой главе мы научились пользоваться ключевым параметром программы интегрирования SMAX. Статистика использования этого параметра для расчетов фрагмента ПРИВОД показывает, что сокращение вычислительных затрат при его грамотном использовании может быть весьма существенным.
7. Для оперативного контроля хода расчета можно и нужно использовать статистическую информацию, выдаваемую программой интегрирования на экран дисплея по ходу расчета. В случае, если статистика результатов будет неудовлетворительной (много потерянных шагов), программа интегрирования может быть прервана, и ее параметры скорректированы.
8. Настройка программы интегрирования (значения ключевых параметров по умолчанию) для разных экземпляров комплекса PRADIS может быть различной. В частности, настройка вашего комплекса может отличаться от настройки комплекса, использованного для экспериментов при написании этого документа.
9. Отладку некоторых фрагментов (например, связанных с анализом механизмов) удобно производить с использованием средств изображения объекта. В этой главе мы научились получать изображение объекта "по умолчанию", масштабировать его и определять положение наблюдателя.
10. Правила хорошего тона.
а) Все списки параметров не только удобно (с точки зрения дальнейшего использования средства $REPLACE), но и необходимо (с точки зрения человека, который будет работать с вашей моделью) описывать в отдельных разделах описания данных.
б) Для определения списков параметров, содержащих более одного параметра, рекомендуется использовать возможность формирования составных списков параметров (т.е., списков параметров, состоящих из ранее определенных списков параметров).
в) При создании программ большого размера можно пользоваться инструкцией включения файла в текст программы ($INCLUDE). Во многих случаях это позволяет структурировать текст программы и облегчить его понимание. Эта инструкция полезна также в случае автоматизированной подготовки данных для модели с помощью автономных программ (как это было в примере с подготовкой данных для профиля кулачка).
6. ДОПОЛНИТЕЛЬНЫЕ ВОЗМОЖНОСТИ УПРАВЛЕНИЯ РАБОЧЕЙ ПРОГРАММОЙ
6.1. ИЗОБРАЖЕНИЕ ИСПОЛНИТЕЛЬНОГО МЕХАНИЗМА
Изображения исполнительного механизма, полученного "по умолчанию", (такого, как в предыдущей главе), может оказаться достаточно для отладки текста описания объекта. Однако, часто требуется получать изображения объекта, имеющие более "товарный" вид (скажем, вам в спину дышит начальство, или нужно соорудить коммерческую прикладную систему). Иногда расширенные возможности раздела SHOW могут пригодиться для детального рассмотрения движения части или частей исследуемой системы в определенном масштабе или определенном ракурсе.
Здесь мы проиллюстрируем эти возможности средств изображения объекта в ходе расчета на примере исполнительного механизма технологической машины из предыдущей главы.
На первом этапе мы ставим перед собой цель "облагородить" изображение механизма и сделать его более информативным. Для этого:
1) получим изображения составных частей исполнительного механизма разными цветами;
2) в сочленениях изобразим шарниры, покажем опоры кривошипа и коромысла;
3) изобразим ползун и направляющие.
6.1.1. Управление составом и цветом изображения для слоя
Для решения первой задачи раздел $SHOW в программе из предыдущей главы изменим таким образом, чтобы изображения различных элементов исполнительного механизма попали в различные слои изображения. Этого можно добиться явным описанием содержимого каждого из слоев. Вначале цвета слоев можно задать по умолчанию (0), но оставить возможность для их изменения с помощью REPLACE (т.е., задавать отдельными списками параметров). С целью более компактной записи описания каждого слоя (по сравнению с описанием, использованным в конце предыдущей главы) объединим три первых списка параметров, входящих в описание параметров слоя изображения, в единый список параметров. Тогда в разделе DATA появятся инструкции:
Цвет изображения кривошипа = 0
Цвет изображения шатуна = 0
Цвет изображения коромысла = 0
Цвет изображения рычага = 0
Параметры слоя = Диаметр окружности,
Центр экрана, Вспомогательные точки;
Описание изображения объекта с выделением каждого из элементов исполнительного механизма в отдельный слой будет таким:
$ SHOW
Кривошип 'LAYER (Кривошип ;Параметры слоя,
Цвет изображения кривошипа)
Шатун 'LAYER (Шатун ;Параметры слоя,
Цвет изображения шатуна)
Рычаг 'LAYER (Рычаг ;Параметры слоя,
Цвет изображения рычага)
Коромысло 'LAYER (Коромысло ;Параметры слоя,
Цвет изображения коромысла)
Если значения параметров, относящихся к цвету изображения, оставлять нулевыми, то элементы каждого слоя будут изображаться своим цветом. Причем, номер цвета соответствует порядковому номеру слоя в описании изображения объекта. В PRADIS принят следующий порядок следования цветов (Таблица 6.1):
Таким образом, первый слой ("Кривошип") будет иметь желтый цвет, второй слой ("Шатун") - зеленый и т.д. Цвет слоя пользователь может определять явно, задавая номер цвета в соответствии с приведенным выше списком. Однако, прежде чем варьировать цветами изображения, есть смысл посмотреть, что получилось. Для этого внесем описанные выше изменения в текст программы TEST5M, запишем измененную программу в файл TEST6M и выполним формирование и расчет модели.
Таблица 6.1. Номера цветов в PRADIS.
|
Номер |
Цвет |
Номер |
Цвет |
|
1 |
желтый |
8 |
грязно-зеленый |
|
2 |
ярко-зеленый |
9 |
фиолетовый |
|
3 |
светло-коричневый |
10 |
темно-зеленый |
|
4 |
розово-красный |
11 |
светло-красный |
|
5 |
светло-синий |
12 |
синий |
|
6 |
бело-голубой |
13 |
серый |
|
7 |
темно-красный |
>13 |
белый |
Теперь представим себе эстета, желающего окрасить коромысло в белоголубой цвет, а шатун - в синий. Тогда этот субъект, если он, конечно, ценит свое время, должен осуществить замену параметров в сформированной модели (используя REPLACE) и запуск задания для уже сформированной модели. Если свое время он не ценит, то может заменить параметры в тексте программы TEST6M и выполнить новое формирование модели (т.е., пройти через этапы трансляции, факторизации и т.д.).
Авторы на своем компьютере предприняли следующие действия:
1) Написали задание для замены параметров в уже сформированной модели:
$ REPLACE :
Цвет изображения шатуна = 6
Цвет изображения коромысла = 5
$ RUN
Автономный анализ механизма 'SHTERM (END=2, SMAX=0.1)
$ PRINT :
Результаты расчета ' DISP ()
$ END
2) Записали это задание в файл T6M.
3) Выполнили команду
> SLANG T6M TEST6M
Один методический совет. Если вы работаете с моделью, и цель вашей работы состоит в подборе тех или иных параметров, то почти наверняка вы будете пользоваться средством $ REPLACE - так удобнее и быстрее. Как правило, по окончании работы с моделью или по окончании какого-либо этапа этой работы файл, содержащий выполняемый модуль рабочей программы, файл заменяемых параметров и файлы результатов удаляются пользователем с магнитного носителя, так как занимают много места. Файлы типа T6M тоже живут недолго. В этой ситуации, отложив на какое-то время работу с моделью, можно через некоторое время по неосторожности утратить информацию об уже проделанной однажды работе. Лучше взять за правило нужные параметры сохранять в исходном тексте описания модели объекта и/или отражать историю работы с этой моделью в комментариях (они почти не сказываются на скорости обработки, а пользу приносят неоценимую). Совсем уже недостижимый идеал - оставлять в том же каталоге, что и текст модели, документ, содержащий результаты работы с моделью (авторы достигали идеала считанные разы при особо важных расчетах).
Высказанные выше соображения становятся еще более актуальными, если вы обнаружили в тексте исходного задания ошибку в данных и для ускорения получения результата используете средство $ REPLACE. Тогда лучше всего выполнить эту работу параллельно - создать задание для замены параметров в уже сформированной модели, содержащее раздел замены параметров, и по ходу дела исправить параметры в тексте исходного описания объекта.
Нужно также не упускать из виду, что замена параметров с помощью $REPLACE действует только во время текущего расчета. Так, если в файле T6M удалить раздел замены параметров и вновь запустить это задание для модели TEST6M, то коромысло опять порозовеет, а шатун позеленеет.
Еще одно наблюдение, которое можно было сделать по ходу этого расчета. Изменение пользователем цвета некоторых слоев не приводит к изменению цветов остальных слоев, принимаемых по умолчанию. Так, цвет рычага по-прежнему остался коричневым, а кривошипа - желтым.
6.1.2. Использование нестандартных графических образов
Поскольку мы уже использовали все возможности по "молчаливому" изображению механизма, для дальнейшего улучшения картинки воспользуемся так называемыми "нестандартными" графическими образами.
Несколько слов по поводу общих принципов, положенных в основу подсистемы изображения объекта. Поскольку предполагается, что в большинстве случаев модель объекта состоит из элементов, то изображение объекта строится из изображений элементов, составляющих модель. Итак, "атомом" изображения служит графический образ элемента. Графические образы элементов могут входить в изображение объекта тогда и постольку, поскольку модель какого-либо элемента входит в общую математическую модель объекта. При этом одной модели элемента не обязательно соответствует только один графический образ.
Исходя из этого, уже при реализации программ графических образов закладывается возможность их использования для изображения движения того или иного конкретного элемента (или элементов одного рода). В наибольшей степени эта возможность определяется количеством степеней свободы элемента. Количество степеней свободы для модели и графического образа должно быть одинаковым. Так, графический образ, служащий для изображения стержневого элемента, окажется непригодным для изображения балки или треугольника.
В каждой модели объекта на языке PRADIS обязательным образом присутствует условно неподвижное тело, с которым связана система координат. Как следует из предыдущего изложения, это тело не указывается явно при описании структуры. Однако, степени свободы, связанные с ним, перечисляются в подразделе #BASE. С системой координат в изображении объекта также могут быть связаны один или несколько графических образов.
Всего можно выделить несколько разновидностей графических образов:
1) Графические образы, связанные с системой координат. Они служат для изображения окружения, в котором движется описываемый объект. Графические образы этой группы не могут быть использованы для изображения каких-либо движущихся элементов изображения. Для включения в изображение объекта графического образа, связанного с системой координат, нужно задать имя образа и его параметры.
2) Графические образы элементов "по умолчанию". Имя такого графического образа формируется по определенным правилам из имени соответствующей модели элемента. Для включения такого графического образа в изображение объекта требуется просто указать идентификатор элемента, изображение которого нужно построить, или потребовать изображения всех элементов объекта, имеющих графические образы по умолчанию (все это уже было сказано выше). В общем случае, образы этой группы могут служить для изображения нескольких элементов одного рода (например, разновидностей плоского стержневого элемента). Графические образы "по умолчанию" могут существовать только для элементов, при описании которых явно задается геометрия (т.е., в основном элементов, совершающих плоское и пространственное движение - балки, стержни, пластины и т.д.).
3) Нестандартные графические образы. Образы этого типа, как правило, тоже могут быть использованы для изображения нескольких элементов, но это не обязательно должны быть элементы одного рода. Здесь принципиально возможно, например, реализовать один образ для изображения различных элементов, имеющих одинаковое количество степеней свободы. Для включения нестандартного графического образа в изображение объекта нужно указать идентификатор изображаемого элемента, имя используемого для его изображения графического образа и его параметры. Во многом вызов нестандартных графических образов схож с вызовом графических образов для изображения окружения, за исключением того, что для них указывается идентификатор элемента, которому образ соответствует. При использовании нестандартных графических образов пользователь должен внимательно изучить информацию, для изображения каких элементов может использоваться каждый конкретный графический образ.
Начало пункта 6.1.2. характеризовалось достаточно высоким уровнем плотности информации, так что даже авторы "запарились". На первый взгляд все это ужасно сложно. Понятно только, что, используя средства изображения объекта комплекса PRADIS, Рафаэлем или, скажем, Пикассо не станешь. Последнее утверждение справедливо, конечно, но безотносительно к комплексу - чтобы стать Рафаэлем, нужно быть Рафаэлем. А что касается использования "нестандартных" графических образов, то мы надеемся, что все разъяснится при рассмотрении нашего примера.
До сих пор при изображении объекта в ходе расчета мы пользовались только графическими образами элементов "по умолчанию". Теперь последовательно изучим возможности описания изображения объекта с использованием неподвижных и нестандартных графических образов.
|
|
|
|
Рис. 6.1. |
Графический образ неподвижной опоры: а) геометрические параметры б) изображения опоры при различных значениях параметра Alfa |
Сначала изобразим опоры. Сделаем это, используя графический образ неподвижной опоры с шарниром - OPORAD. Краткую справку по этой программе можно получить стандартным способом (ARM ? OPORAD). Информация, содержащаяся в справке, поясняется рис.6.1. Вообще говоря, для того, чтобы изобразить опору в том виде, в котором она изображена на этом рисунке, требуется гораздо больше размеров. Однако, увеличение количества параметров, которые не влияют на расчет по существу, и в то же время необходимы для создания приемлемого изображения, нежелательно. Поэтому для базовых графических образов широко используется параметризация. Использование этого подхода часто позволяет для формирования изображения обойтись только параметрами, необходимыми для включенных в структуру анализируемого объекта моделей элементов (они все равно присутствуют в разделе DATA), или ограничиться очень небольшим количеством дополнительных параметров. Возвращаясь к изображению опоры, можно сказать, что собственные размеры опоры определяются так называемым "характерным размером" - радиусом окружности с центром в точке с координатами Xc и Yc, проходящей через основание опоры, как это показано на рис. 6.1а. На рисунке эта окружность изображена пунктирной линией. Если в модель объекта включена модель элемента "шарнир", то диаметр шарнира задается в списке параметров этой модели элемента. Если шарниры отсутствуют в структуре модели, как в нашем случае, то часто прибегают к приему, при котором все подвижные шарниры и шарниры неподвижных опор изображают кружками одного размера, что существенно сокращает количество параметров, которые нужно задавать. Координаты опоры в глобальной системе координат (Xc, Yc) присутствуют в модели объекта для определения положения того элемента, который в этом месте соединяется с опорой (в нашем случае это - точка O, с которой соединяется кривошип, и точка E, с которой соединено коромысло). Для подавляющего большинства случаев опору можно изобразить параллельно одной из осей координат экрана (как это показано на рис. 6.1.б ). В то же время, если определять для таких положений точное значение угла в радианах, это вызовет у среднего человека (не умеющего получать в уме шесть-семь знаков после запятой при умножении на число p) определенные сложности. Задание угла в градусах спасает только отчасти, так как для большинства программ в комплексе принято задание углов в радианах. В данном случае было решено пойти на ограничение, при котором значение угла, задающего положение опоры, округляется до ближайшего значения из ряда 0, p/2, p, 3/2p. Изображение опоры на экране при различных значениях параметра Alfa показано на рис.6.1б.
Для изображения опоры кривошипа зададим значение параметра Alfa=5, а для опоры коромысла Alfa=0. Размеры опор и шарниров выберем такими, чтобы они соответствовали изображениям рычагов механизма (картинка должна "смотреться"). По нашему мнению, для размера опоры - это примерно 0.10, для диаметра шарнира - 0.05. Значение координаты Zc, которое требуется для полного определения положения опоры в пространстве, в данном случае безразлично. Поэтому Zc=0. Изображения опор опишем в отдельном слое.
С неподвижной системой координат будет связано также изображение направляющей ползуна. Просмотр имеющихся в базовой библиотеке графических образов показывает, что для получения неподвижного изображения какого-либо сложного плоского контура может быть использована программа KONTUR, в качестве параметров которой задаются десять пар координат точек, определяющих этот контур. Средний ( = ленивый в хорошем смысле этого слова, т.е. не желающий тратить свое время по пустякам) пользователь PRADIS, вставший перед перспективой определить для учебного задания десять (!) пар абстрактных точек, единственной целью подбора которых является украшение изображения, не будет этим заниматься. Поскольку координаты контура, при этом специально найденные для этого случая авторами в ближайшем кустарнике, будут играть определенную роль в дальнейшем изложении, мы предлагаем для стойки пресса использовать авторский дизайн. (Обратите внимание, что при этом как бы делается одолжение пользователю). Координаты точек контура стойки приведем ниже в блоке данных вновь сформированной программы.
Перейдем к изображению подвижных элементов. Просмотр списка графических образов базовой библиотеки с целью найти образ для изображения подвижных шарниров приводит нас к следующему результату:
1) для изображения шарниров в нашей задаче можно использовать графический образ точки, движущейся в плоскости (DOTD, рис.6.2.);
2) этот графический образ нельзя связать ни с одним из элементов, присутствующих в структуре модели механизма (DOTD имеет три степени свободы, стержень - четыре, треугольник и балка - по шесть).
|
|
|
|
Рис. 6.2. |
Геометрические параметры графического образа DOTD. |
В общем, эта ситуация является прямым следствием упрощения модели. Мы ее собрали таким образом, чтобы не учитывать свойства реальных шарниров в объекте, но изображать эти шарниры хотим. Одним словом, "и водицы испить, и портки не замочить". Втирание очков вызывает обычно дополнительные непроизводительные трудозатраты. Минимальной кровью в данном случае можно обойтись, введя в модель механизма для учета инерционных свойств шарниров точечные инерционные элементы, совершающие плоское движение (элемент MD). Если мы считаем, что они не скажутся особо на динамических процессах, то можно задать и массу и момент инерции шарниров равными 0. Но, раз уж нам все равно придется вносить этот элемент в описание структуры модели, зададим массу шарниров соизмеримой с массами рычагов. Например, 0.03 кг. Момент инерции, учитывая, что угловые координаты в модели во всех подвижных узлах все равно отсутствуют, примем равным 0. Естественно, что в дальнейшем, в результате якобы предполагаемой конструктивной проработки узла, эти параметры должны уточняться.
Идентификаторы новых элементов, появившихся в описании структуры исполнительного механизма, будем формировать в соответствии с буквенными обозначениями соответствующих точек рис. 5.1. ("Шарнир A","Шарнир B" и т.д.). При таком изменении структуры модели можно теперь связать с этими элементами графический образ DOTD, задавшись, для удобства, теми же размерами шарниров, что и для опор. Графический образ DOTD позволяет изображать как круг (параметр заполнения в этом случае должен быть задан равным 1), так и окружность (параметр заполнения равен 0).
Поскольку мы здесь коснулись понятия "минимальной крови" (налево пойдешь - лошадь потеряешь), то можно указать и максимально кровавый путь (направо пойдешь - головы лишишься). В данном случае это изучение документа "Включение программ пользователя в библиотеки комплекса. Руководство пользователя.", и написание фирменного графического образа шарнира, который можно связать с нужными элементами.
Для изображения ползуна можно использовать графический образ прямоугольника, движущегося в плоскости (RECTD). Его параметры задаются по тому же принципу, что и для элемента DOTD (координаты центра, размеры - высота и ширина). Исключением является то, что этот образ всегда "заливается" текущим цветом изображения. Как и в случае с использованием DOTD, его необходимо связывать с элементом MD, т.е. для моделирования ползуна использовать не модель M (имеет одну степень свободы), а MD (три степени свободы, поперечная и угловая степени свободы связаны с системой координат).
И, наконец, порядок описания слоев изображения. При его определении следует учитывать, что слой изображения, описанный раньше, и рисоваться будет тоже раньше. Если говорить о нашей программе, то есть смысл вначале нарисовать неподвижные опоры и контур направляющей, затем - ползун, рычаги механизма, и, наконец, подвижные шарниры.
Параллельно приведенным в этом пункте рассуждениям нами вносились изменения в текст файла TEST6M. Учитывая, что, начиная с пятой главы, в качестве примеров приводятся объемистые программы, за которыми становится не видно живого текста руководства, от авторов поступило предложение приводить только фрагменты текстов этих программ с наиболее существенными изменениями. При этом на пользователя возлагается ответственность за получение окончательного текста программы. Поскольку читателей на момент принятия решения поблизости не было, предложение набрало необходимое большинство голосов. Поэтому здесь приводим наиболее существенные изменения описания объекта и его изображения, а также обещанные выше координаты контура стойки:
$ DATA
* * *
Координаты стойки = 0.5 , 0.1, 0.5 , 0. ,
0.75,-0.2, 0.75,-0.4,
0.601,-0.65, 0.601,-1.55,
0.0 ,-1.55, 0. , -1.65,
0.9 ,-1.65, 0.9 , 0.;
* * *
$ FRAGMENT: МЕХАНИЗМ
# BASE: * * *, 15
# STRUCT:
* * *
Шарнир A 'MD (4 5 6; 0.5, 0)
* * *
Ползун 'MD (13 14 15; Масса ползуна, 0)
* * *
$ SHOW
Опоры 'LAYER ((OPORAD; Точка O,0., Размер опоры, 5,
Диаметр шарнира),
(OPORAD; Точка E,0., Размер опоры, 0,
Диаметр шарнира);
Параметры слоя,
Цвет изображения опоры )
Ползун 'LAYER (Ползун(RECTD;Точка D,Ширина ползуна,
Высота ползуна);
Параметры слоя,
Цвет изображения ползуна )
Стойка машины'LAYER ((KONTUR; Координаты стойки);
Параметры слоя,
Цвет изображения стойки )
* * *
Шарниры 'LAYER (Шарнир A(DOTD;Точка A,Диаметр шарнира,1),
Шарнир B(DOTD;Точка B,Диаметр шарнира,1),
Шарнир C(DOTD;Точка C,Диаметр шарнира,1),
Шарнир D(DOTD;Точка D,Диаметр шарнира,1);
Параметры слоя,
Цвет изображения шарниров )
* * *
В качестве необходимого примечания отметим, что звездочки повсюду в тексте программы не являются частью текста на языке PRADIS. Это - следы ножниц, руководимых авторами. Из рабочего текста программы TEST6M было вырезано знакомое читателю и оставлены только некоторые новые элементы программы, о которых шла речь в этом пункте.
6.1.3. Связь слоя изображения с подвижной системой координат
Вы сидели когда-нибудь на шатуне механизма? Иногда любопытно посмотреть, как ведет себя окружающая обстановка (в данном случае, естественно, на модели, без риска зашибиться), если вы совершаете какое-нибудь сложное движение. Здесь - плоское (но ничто не мешает вам на досуге собрать пространственный механизм, и прокатиться уже пространственно и еще более нелинейно).
При описании изображения в PRADIS-программе можно связать какие-либо конкретные слои изображения с теми или иными степенями свободы модели. Для этого вернемся к рис.5.6. и вспомним, что точка зрения наблюдателя на объект задается положением точек As (здесь помещается наблюдатель), Bs и Cs (задают положение экрана и его вращение). Индекс "s" здесь используется для того, чтобы не спутать обозначения этих точек с характерными точками механизма. Если мы хотим систему координат сделать подвижной, то в этом случае уже не удастся так лихо определять начальное положение вспомогательных точек, как это было ранее, даже если изображение объекта находится в плоскости OXY. Лучше всего их связать с какими-либо реальными точками изображения. В нашем случае предлагается наблюдателя посадить над точкой C шатуна (абсцисса и ордината точек As и Cs будут равны абсциссе и ординате точки C шатуна, аппликата точки As будет равна, например, 1, точки Cs - 0), а точку Bs поместить в точку D. Кроме того, нужно связать слой изображения со степенями свободы этих точек (C и D шатуна). Для определения перемещения системы координат, связанной со слоем изображения, потребуется задать девять степеней свободы - X,Y,Z для каждой из точек As,Bs,Cs. В нашем случае степень свободы, определяющая движение каждой из этих точек по оси Z, будет связана с базовой системой координат. Степени свободы по осям X и Y для точек As и Cs нужно связать с соответствующими степенями свободы точки C, Bs - со степенями свободы точки D. Порядок задания степеней вободы точек As, Bs и Cs при описании слоя изображения такой же, как и при задании начальных координат этих точек - Xc,Yc,Zc, Xa,Ya,Za, Xb,Yb,Zb.
С учетом сделанных изменений описание слоя для изображения, например, кривошипа в системе координат, связанной с шатуном, будет выглядеть так:
Кривошип 'LAYER (Кривошип; Параметры слоя,
Цвет изображения кривошипа;
11 12 1 11 12 1 13 14 1 )
Вернувшись к тексту задания TEST6M, внесем в него изменения с целью изобразить механизм в подвижной системе координат (для всех слоев изображения будут задаваться такие же степени свободы, как и для слоя в приведенном выше примере). Запишем полученное задание в файл TEST63M. Любопытствующие могут выполнить для задания TEST63M команду SLANG и посидеть на шатуне во время движения (авторы не отказали себе в удовольствии).
6.2. УПРАВЛЕНИЕ ТОЧНОСТЬЮ РЕШЕНИЯ СИСТЕМЫ ДУ
По ходу отладки модели механизма продолжим здесь изучение вопросов управления работой программы интегрирования. В этом подразделе рассмотрим ключевые параметры, управляющие точностью решения системы дифференциальных уравнений, и связанные с этим особенности вычислительного алгоритма.
6.2.1. Окончательный текст программы, реализующей модель механизма
Для глобальных целей, сформулированных в главе 5 (осуществление нескольких итераций проектного расчета машины с последовательным уточнением ее параметров) и выполнения того, что было обещано в заголовке подраздела 6.2, будем ваять в этом пункте текст окончательной программы для анализа механизма.
В качестве основы для окончательного текста используем программу из файла TEST63M. Уберем в этом тексте связь слоев изображения с подвижной системой координат (чтобы не закружилась голова), а в подраздел OUTPUT добавим описание выходных переменных, которые могут понадобиться нам для анализа работоспособности механизма. При этом оставим в стороне вопрос с расчетом кривошипа и рычага (в реальности они будут представлены, видимо, особыми конструктивными элементами, расчет которых специфичен. Например, кривошип может быть выполнен в виде эксцентрикового колеса или коленчатого вала). Для нас важной будет информация о величине продольных усилий в коромысле и шатуне, которые в этих элементах определят величину сжимающих (растягивающих) напряжений. Так как модель стержня не воспринимает поперечные нагрузки, интересующее нас усилие может быть выведено с помощью программы ROUT (она рассчитывает результирующую величину как квадратный корень из суммы квадратов составляющих). Поскольку усилие и напряжение связаны законом Гука ( Sigm = P/F = = 1/F * P), то в качестве масштаба для вычислений может быть выбрана величина 1/F, и тогда будет рассчитываться непосредственно величина напряжения. Таким образом, в блоке описания данных и подразделе OUTPUT этого задания появятся следующие описания:
$ DATA :
Масштаб пересчета напр.шатуна = 1.E4
Масштаб пересчета напр.кором. = 1.E4
* * *
$ FRAGMENT : МЕХАНИЗМ
* * *
# OUTPUT :
Напряжение в шатуне 'ROUT (I:Шатун (1), I:Шатун (2);
Масштаб пересчета напр.шатуна)
Напряжение в коромысле'ROUT (I:Коромысло(1), I:Коромысло(2);
Масштаб пересчета напр.кором.)
* * *
Учитывая упрощенный характер нашего иллюстративного примера, этого нам может оказаться достаточно.
Непосредственно для экспериментов с погрешностью расчетов авторы добавили в свое задание расчет скоростей по всем степеням свободы механизма. При анализе всей машины расчет этих выходных переменных в программе будет отсутствовать.
6.2.2. Ключевые параметры, определяющие локальную погрешность интегрирования
Здесь мы более подробно рассмотрим алгоритм оценки и контроля точности решения системы дифференциальных уравнений, используемый в комплексе PRADIS. Вообще говоря, математическая модель технического объекта представляется в виде системы дифференциальных уравнений. Однако, без нарушения общности, мы можем здесь рассмотреть численное решение одного дифференциального уравнения
F (X, X', X", T) = 0 (6.1),
имея в виду, что решение системы дифференциальных уравнений получается аналогично. Как известно, решением уравнения (6.1) является большое количество интегральных функций X(t), отличающихся друг от друга произвольными постоянными. Эти произвольные постоянные должны быть определены из начальных условий. Таким образом, получаем функцию, отвечающую дифференциальному уравнению (6.1) и заданным начальным условиям (Xo и X'о).
Погрешность численного решения определяется тем, что на каждом шаге интегрирования интегрируемая функция заменяется отрезком или кривой (в зависимости от применяемой формулы интегрирования). Это, вообще говоря, вызывает переход к новой интегральной функции, удовлетворяющей уравнению (6.1), но не удовлетворяющей заданным начальным условиям. Погрешность решения, полученная на шаге интегрирования, называется локальной погрешностью. От шага к шагу эта погрешность накапливается, что ведет к увеличению расстояния между точным решением, и положением интегральной функции на текущем шаге - т.е., к увеличению накопленной погрешности (или еще говорят - глобальной погрешности) решения. Допустим, при решении какой-либо задачи было сделано несколько шагов интегрирования и к N-му шагу интегрирования накоплена определенная погрешность.После этого интегрирование стало абсолютно точным. Даже при этих условиях накопленная погрешность решения не будет оставаться неизменной. Ее величина зависит от поведения интегральной кривой в окрестности рассматриваемой точки. Поэтому, в зависимости от конкретных условий, локальная погрешность шага интегрирования может по-разному влиять на накопленную погрешность. Если характер изменения решения д.у. таков, что увеличение значения функции приводит к увеличению значения ее производной (= уменьшение функции - к уменьшению производной, т.е. знаки первой и второй производной совпадают), то расстояние между интегральными кривыми увеличивается. Так ведут себя функции типа Y=X**N при X > 0, Y=EXP(X) на всей области определения и т.д. В этом случае накопленная погрешность решения больше суммы локальных погрешностей каждого шага интегрирования. Естественно, что с увеличением крутизны функции эта разница возрастает. Кроме того, величина уже накопленной погрешности решения будет увеличиваться даже при отсутствии локальной погрешности. Если же с увеличением значения функции производная уменьшается (знаки первой и второй производной различаются), то накопленная погрешность решения меньше суммы локальных погрешностей всех шагов интегрирования. Так ведут себя функции типа Y=X**N при X < 0, Y=SQRT(X) на всей области определения и т.д.
В комплексе PRADIS, как правило, локальная погрешность решения оценивается относительно скорости. Рис. 6.3. иллюстрирует метод ее определения. Для решения уравнения (6.1) используется один из неявных методов интегрирования (в технических приложениях основным является метод Штермера, для учебных и исследовательских задач часто может использоваться метод Ньюмарка). В любом случае, для неявного метода интегрирования характерно выполнение шага интегрирования в два этапа. На первом этапе осуществляется явный прогноз, на втором - итерационно повторяющаяся коррекция. В скобках заметим, что любой явный метод интегрирования является частным случаем неявного, когда отсутствует коррекция решения. Если говорить о геометрической интерпретации неявного метода интегрирования (рис.6.3), то выполнение прогноза эквивалентно замене интегральной кривой на временном интервале [ti,ti+1] отрезком касательной к ней в точке с абсциссой ti. Второй этап сводится к нахождению угла наклона касательной к интегральной кривой в точке с абсциссой ti+1 и замене интегральной кривой на временном интервале [ti,ti+1] отрезком этой касательной.
Значение скорости, полученное явным прогнозом, обозначим Vp, скорректированное значение скорости - Vc (перед Vc не минус, а тире!).
Здесь, может быть, уместно к слову рассказать один случай из голубого детства по поводу знаков и букв в тексте, допускающих двоякое толкование, а пользователю - немного расслабиться. Один раз учительница сказала ученице, слабо успевающей по математике, что для получения заветной тройки той надо выучить наизусть несколько параграфов из учебника по геометрии. На следующий день, во время экзамена с пристрастием, на вопрос "Какова длина окружности?" было отвечено: "Два Пэ Че", чем и заработано 3 балла - никто не смог устоять на ногах, даже учитель. Итак, еще раз - здесь имелось ввиду тире.
По построению, эти значения (имеется ввиду Vp и Vc, для тех, кто успел забыть) находятся по разные стороны от локально точного значения скорости, лежащего на текущей интегральной кривой. Заметим, что в случае, если на каждом шаге интегрирования получать локально точное значение скорости, то мы не будем уклоняться от точного решения. На самом деле получается погрешность, не превышающая в самом неблагоприятном случае величины Vp - Vc. В качестве оценки абсолютного значения локальной погрешности на шаге интегрирования в PRADIS принимается величина
Di+1 = (Vp - Vc) /2 (6.2)
Из рисунка 6.3 видно также, что уменьшение шага интегрирования приводит и к уменьшению величины локальной погрешности, так как разница между прогнозом и коррекцией при меньшем шаге уменьшается. Поэтому, если текущая локальная погрешность превосходит допустимую погрешность, заданную пользователем, то шаг интегрирования должен быть уменьшен.
|
|
|
|
Рис. 6.3. |
К определению локальной погрешности на шаге интегрирования. |
Однако, в некоторых случаях абсолютную погрешность для оценки точности вычислений использовать неудобно. Это будет происходить всегда, когда абсолютное значение скорости велико. Тогда отличие между прогнозом и коррекцией даже на десятые и сотые доли процента может привести к тому, что абсолютная величина локальной погрешности будет слишком большой. В этом случае для контроля точности полезно использовать значение относительной величины локальной погрешности
ei+1 = D i+1 / Vc (6.3)
Но и эта оценка не является универсальной. В области малых значений скоростей относительная ошибка будет получаться слишком большой, и программа интегрирования начнет сильно мельчить шаг. Хотя это, как правило, не требуется. И действительно, обычного пользователя вряд ли будет волновать вопрос, с какой точностью определено значение скорости - 1% или 100%, если ее текущая величина равна 0.00001 м/с, а амплитудное значение для этого процесса 1м/c.
Итак, исходя из приведенных выше рассуждений, становится понятным, что в области больших значений скоростей для контроля точности получаемого решения предпочтительно использовать относительную погрешность, а в области малых скоростей - абсолютную. Но где грань между большим и малым ? (Обратите внимание, вопрос из серии "Быть или не быть?", "Что есть истина?" и т.д. С одним только этим вопросом можно угодить на Золотые Скрижали Истории Человечества). Поэтому, и имея ввиду роковую беспощадность этого вопроса, для контроля величины локальной погрешности шага интегрирования используется значение абсолютной погрешности, полученной из следующих соображений:
1) Пользователь задает допускаемую величину относительной (в области больших скоростей) и абсолютной (в области малых скоростей) локальной погрешности (соответственно, [e] и [D]).
2) Допускаемое значение абсолютной локальной погрешности для текущего шага интегрирования определяется программой интегрирования по зависимости
[D] = [D] + [e] * Vc (6.4)
3) Для оценки локальной точности шага интегрирования величина Di+1 сравнивается с [D]. Если выполняется соотношение D i+1 < [D], то считается, что требуемая точность достигнута.
Проанализируем выражение (6.4). Если величина скорости Vc велика, то второй член правой части этого выражения, характеризующий влияние относительной погрешности, становится определяющим или соизмеримым с заданной абсолютной погрешностью (конечно, если не задано, что допускаемая абсолютная погрешность решения превосходит максимальное значение скорости, а находится в разумных пределах). Когда же величина скорости Vc мала, влияние этого члена становится пренебрежимо малым, и на оценку погрешности будет оказывать основное влияние допускаемое значение абсолютной погрешности.
Поэтому для задания локальной погрешности интегрирования пользователь может использовать два ключевых параметра программы интегрирования - DRLTX и DABSX. DRLTX задает относительное значение допустимой локальной погрешности (в области больших значений скоростей), а DABSX - абсолютное значение допустимой локальной погрешности (в области малых скоростей). Для определения допустимой абсолютной погрешности шага интегрирования в зависимости от текущего значения скорости используется выражение (6.4).
Еще одно лирическое отступление. Рис. 6.3. может создать впечатление, что значение скорости, полученное прогнозом, точнее окончательного решения, полученного коррекцией. Это происходит потому, что в точке с абсциссой ti значение скорости, являющееся начальным для данного шага интегрирования, уже отличалось от точного решения. При этом отклонение было в ту сторону, которая характерна для неявного метода интегрирования. Поэтому каждый последующий неявный шаг интегрирования будет эту погрешность увеличивать. В случае, если бы интегрирование проводилось явным методом, то скорость в точке с абсциссой ti также была бы найдена с погрешностью.
Однако, ее значение находилось бы по другую сторону от интегральной кривой. Поэтому каждый явный шаг интегрирования эту погрешность также увеличивал бы. Вообще, точности явного и неявного методов интегрирования при использовании формул интегрирования одного порядка одинакова. Другое дело, что явный метод интегрирования отличается некоторыми неприятными особенностями (неустойчивость метода), из-за которых, несмотря на всю его простоту, его использование в серьезных программах является проблематичным.
6.2.3. Численные эксперименты с локальной погрешностью
Используем полученное в пункте 6.2.1 окончательное описание модели механизма для нескольких численных экспериментов с локальной погрешностью.
Характер изменения скоростей по всем степеням свободы механизма таков, что в районах экстремумов интегральные кривые будут резко расходиться. В соответствии с тем, что было изложено в пункте 6.2.2, в этом месте будут наблюдаться максимальные накопленные погрешности. Вдоль остальной интегральной кривой накопленная погрешность должна быть значительно меньше. Если получить "точное" значение скорости в районе экстремума (например, значительно более точным расчетом), то сравнение значений скоростей в экстремальных точках будет характеризовать максимальную величину накопленной погрешности.
Вначале проведем точный расчет, задав DRLTX=1.e-5, DABSX=1.e-5. Будем анализировать две секунды процесса. Накопленную погрешность этого расчета можно оценить, сравнивая максимальное и минимальное значение скорости на анализируемом интервале. Поскольку за это время механизм совершает качание вперед-назад, зависимости для скоростей должны быть симметричны, максимальная и минимальная скорости - равны по абсолютной величине.
По ходу расчета величина шага интегрирования нигде не поднималась до максимально разрешенного. В пределах того шага, который определялся заданной локальной погрешностью, процесс был практически линейным. Количество итераций на шаг интегрирования в среднем (16128+326)/(8118+163)=1.987. По локальной погрешности потеряно 163 шага. Результаты расчетов двух первых экстремумов скоростей по всем степеням свободы механизма приведены в таблице 6.2. Время расчета - 3167 с.
По этим результатам можно сказать, что накопленная погрешность расчета не очень велика, так как разница между амплитудами минимальной и максимальной скоростей около 0.5% или меньше. Поэтому абсолютное значение первого экстремума для наших дальнейших целей можно принять за точное значение экстремума скорости по этой степени свободы (по некоторым степеням свободы это - значение минимума, по некоторым - максимума, т.е. того экстремума, который больше по абсолютной величине).
Таблица 6.2. Экстремумы скорости по степеням свободы механизма, полученные точным расчетом.
|
Степень свободы |
Скорость |
|
|
|
Минимальная |
Максимальная |
|
3 |
-.19009 E+02 |
.19102 E+02 |
|
4 |
-.32736 E+01 |
.32931 E+01 |
|
5 |
-.42931 E+01 |
.43112 E+01 |
|
6 |
-.19009 E+02 |
.19102 E+02 |
|
7 |
-.26446 E+01 |
.26639 E+01 |
|
8 |
-.11539 E+01 |
.11377 E+01 |
|
11 |
-.40192 E+01 |
.40111 E+01 |
|
12 |
-.11734 E+01 |
.11577 E+01 |
|
14 |
-.16707 E+01 |
.16711 E+01 |
Таблица 6.3. Зависимость амплитудных значений скоростей от заданной величины абсолютной локальной погрешности.
|
|
Скорость по степени свободы |
|||||
|
DABSX |
3 |
5 |
8 |
|||
|
|
min |
max |
min |
max |
min |
max |
|
1.e-4 |
-18.345 |
18.826 |
-4.1497 |
4.2418 |
-1.1509 |
1.0605 |
|
0.001 |
-17.720 |
18.621 |
-4.0143 |
4.1904 |
-1.1489 |
0.9939 |
|
0.005 |
-17.110 |
18.267 |
-3.8758 |
4.1121 |
-1.1470 |
0.9229 |
|
0.01 |
-16.479 |
17.948 |
-3.7358 |
4.0379 |
-1.1450 |
0.8531 |
|
0.1 |
-13.688 |
16.651 |
-3.1138 |
3.7335 |
-1.1437 |
0.5939 |
Таблица 6.4. Статистика результатов расчетов.
|
N |
DABSX |
Успешных шагов |
Потери шагов |
Всего итераций |
Время счета (с) |
Итераций на шаг |
|
1 |
1.e-4 |
1304 |
39/0 |
2682 |
510 |
1.997 |
|
2 |
0.001 |
652 |
16/0 |
1382 |
265 |
2.069 |
|
3 |
0.005 |
430 |
23/0 |
1164 |
212 |
2.570 |
|
4 |
0.01 |
309 |
32/1 |
944 |
170 |
2.760 |
|
5 |
-0.10 |
177 |
33/6 |
776 |
132 |
3.593 |
Так, для третьей степени свободы - это 19.102 1/c, для пятой 4.3112 м/с, для восьмой 1.1539 м/с). Кроме того, в нашем дальнейшем анализе несколько ограничим количество рассматриваемых степеней свободы. Будем анализировать скорости по степеням свободы с номерами 3, 5 и 8.
Значение ключевого параметра DRLTX зададим по умолчанию. В нашем варианте комплекса его величина по умолчанию составляла 0.001. Поэтому на точность результатов расчетов будет влиять в основном значение параметра DABSX. Начнем изменять разрешенную абсолютную погрешность, сводя полученные результаты в таблицы 6.3 и 6.4.
Несколько комментариев к расчетам. Здесь, как и предлагалось выше, в качестве оценки накопленной погрешности решения будем использовать накопленную погрешность в районе экстремума скорости.
Во-первых, сравнение первого и второго экстремумов скорости для всех степеней свободы механизма и во всех расчетах показывает, что, как и следовало ожидать, накопленная ошибка интегрирования с течением времени возрастает (т.е., интегрирование этого процесса неявным методом в конечном итоге приведет к затуханию колебаний в системе).
Во-вторых, можно сравнить величину накопленной погрешности с ориентировочной суммой локальных погрешностей всех шагов интегрирования. Если говорить о третьей степени свободы, то для первого расчета сумма локальных погрешностей шагов интегрирования (ориентировочно 10-4*1304 = 0.13) значительно меньше накопленной погрешности решения в районе второго экстремума (ориентировочно 19.102-18.345 = 0.757). Для второго расчета эта тенденция сохраняется, хотя разница уменьшилась (соответственно, 0.652 и 1.382). В третьем и четвертом расчетах накопленная ошибка и сумма локальных погрешностей шагов интегрирования примерно одинаковы. Для пятого расчета сумма локальных погрешностей шагов интегрирования внушительно больше накопленной локальной погрешности (17.7 и 5.4). Это происходит потому, что в районе экстремума пик скорости можно сравнить с иголкой. И чем ближе мы подбираемся к экстремуму, тем больше расходятся интегральные кривые. Поэтому эскалация точности влечет за собой непропорциональное увеличение вычислительных затрат. Отсюда можно сделать вывод: по возможности не суй нос в узкие щели, могут отдавить! Ну а если отложить шутки в сторону, то можно сказать, что определение точного значения интегральной функции в районе пиковых экстремумов с использованием метода Штермера является дорогостоящей затеей. Если "сильно вам неймется", можно для этих целей использовать метод Ньюмарка. Он имеет более высокий порядок точности, и при сравнимых вычислительных затратах найденные им решения будут точнее. Но при этом вы должны быть готовы к тому, что ваш нос будет попадать во все выемки на этом пути - даже мельчайшие, отслеживая по-возможности все колебания, в том числе паразитные и никак вас не интересующие в данный момент. А если, не дай бог, зазорчики или удары ...
В третьих, обратим внимание на тот факт, что снижение требований к точности решения приводит к ухудшению сходимости решения системы нелинейных уравнений. Это и понятно - в качестве начального приближения на каждом шаге интегрирования берется решение, полученное на предыдущем шаге. Поэтому, чем больше шаг, тем больше различаются начальное приближение и искомая точка, и для решения системы нелинейных уравнений требуется большее количество итераций. В четвертом и пятом расчетах на некоторых шагах интегрирования появилась несходимость решения системы нелинейных уравнений за максимально допустимое количество итераций (в нашем случае было 5).
|
|
|
|
Рис. 6.4. |
Влияние ключевого параметра DABSX на результаты интегрирования. |
На рис. 6.4. приводятся результаты интегрирования скорости по третьей степени свободы - точное решение (DABSX=1.E-5) и решения для разных значений ключевого параметра DABSX.
В целом, оптимальное значение допускаемой абсолютной погрешности для этого расчета лежит, видимо, в пределах 0.01...0.005, если пользователя удовлетворит умеренная величина накопленной погрешности. Дальнейшее увеличение точности потребует более существенного увеличения вычислительных затрат.
6.3. РАСЧЕТ ТЕХНОЛОГИЧЕСКОЙ МАШИНЫ
Как предлагалось в пункте 5.3.6, соберем окончательный текст программы для моделирования всей машины с использованием инструкции препроцессора $INCLUDE. Поскольку эта программа будет находиться в нескольких файлах, целесообразно для работы с ней сформировать новый каталог, например, MASHTST. Файл PRIVOD будет содержать описание данных и структуры привода машины, MEHAN - механизма, VISUAL - описание изображения. Текст основной программы будет находиться в файле TEST63.
Содержимое файла PRIVOD должно отличаться от программы описания привода, полученной в пятой главе. Дело в том, что программа из пятой главы имеет небольшие размеры. Поэтому было почти безразлично, разгонять маховик с нулевой скорости, или задать начальную скорость маховика равной номинальной скорости двигателя. Для бОльших моделей это может играть существенную роль. Во фрагменте PRIVOD, который мы будем использовать здесь, начальная скорость вала двигателя задается пользователем. Это делается с использованием модели VN (элемент, задающий начальную скорость той степени свободы, с которой он связан). Естественно, что в файле PRIVOD отсутствуют разделы RUN, PRINT и заголовок $END.
Файл MEHAN содержит описание структуры фрагмента МЕХАНИЗМ, полученное в пункте 6.2.1 (без разделов SHOW, RUN, PRINT и заголовка END). Как говорилось выше, здесь нам уже не понадобится выводить скорости по различным степеням свободы механизма.
Файл VISUAL содержит описание изображения объекта в ходе расчета из той же программы п. 6.2.1.
К описанию объекта, приведенного в 5.3.6 и полностью использованного в программе TEST63, мы добавили описание задания на расчет одного рабочего цикла машины и задание на отображение выходных переменных (как это было сделано в 5.3.5 для программы, не использующей инструкции $INCLUDE).
Все данные, относящиеся к описанию геометрии объекта, были перенесены из блока данных исполнительного механизма в глобальный блок данных. Это нужно сделать потому, что раздел описания изображения объекта относится ко всему объекту, а не к отдельным фрагментам. Поэтому в этом разделе доступны только те данные, что относятся к глобальному фрагменту.
Как всегда, запустим процедуру выполнения задания и проведем визуальный осмотр на месте.
По результатам первого расчета бросается в глаза два факта: 1) Муфта слишком немощна, что приводит к ее запоздалому полному включению (уже после выполнения рабочего хода). Кроме того, при каждом новом рабочем ходе она проскальзывает (в момент максимального ускорения ползуна). 2) Рычаги исполнительного механизма испытывают небольшие нагрузки (меньше 10 МПа).
Если подходить к "проектному расчету машины" в первом приближении честно, хотя бы на уровне сопротивления материалов, нужно рычаги ослаблять. Примем в качестве ориентировочной величины допускаемых напряжений величину 100 МПа. Но при ослаблении шатунов необходима их проверка на устойчивость. В рассматриваемой задаче это трудно сделать средствами комплекса, так как решение вопроса устойчивости предполагает учет в модели геометрии поперечного сечения рычагов. Либо задачу нужно переформулировать (подробно описывать геометрию поперечного сечения шатуна и коромысла, что не входило в наши планы при написании этого документа), либо сделать прикидочные расчеты на близлежащем заборе. Мы предлагаем здесь пойти по второму пути. Полагая, что рычаги в сечении, достаточно удаленном от шарниров, имеют сплошное квадратное сечение, получим:
- радиус инерции сечения i = SQRT(J/F) = SQRT(a**2/12) = 3.46*a
- гибкость рычагов Lam = mu*l/i = 0.29*mu*l/a = 0.29*l/a
(mu для этого случая = 1)
Для шатуна (учитывая, что его длина - 0.763 м), получим Lam = 22.12 (коэффициент снижения допускаемого напряжения около 0.95), для коромысла - 11.36 (коэффициент близок к единице). Если уменьшать площадь поперечного сечения рычагов в 4 раза, получим длину стороны сечения 0.005, и гибкости будут: у шатуна - 44 (коэффициент снижения допускаемых напряжений = 0.62, если принять, что материал рычагов - чугун; величина допускаемых напряжений - 62 МПа), у коромысла - 22 (коэффициент около 0.95, допускаемые напряжения - 95 МПа). При этом нужно не забыть скорректировать площади поперечного сечения рычагов и масштабы пересчета усилий в напряжения.
По поводу муфты мы будем варьировать только одним параметром - средним диаметром фрикционных накладок (считаем, что коэффициент трения определяется материалом трущихся поверхностей и задан). Максимальный момент на втором валу привода - 32 н*м. Для его обеспечения муфта должна иметь средний диаметр полумуфт 0.640 мм (32 /500/0.2 * 2).
С учетом предлагаемых изменений раздел REPLACE для замены параметров в уже сформированной модели будет выглядеть так:
$ REPLACE :
Масштаб пересчета напр.шатуна = 4.E4
Масштаб пересчета напр.кором. = 4.E4
F коромысла = 0.25 E-4 ; F шатуна = 0.25 E-4
Средний диаметр дисков трения = 0.640
Как обычно, дополним это описание разделами RUN и PRINT и выполним команду запуска задания для уже сформированной модели:
> SLANG T63 TEST63
На экране после прохождения листинга появляется сообщение об отсутствии в тексте программы синтаксических ошибок и, сразу после этого, - сообщение программы управления базой данных (S 145) о том, что ни один из списков параметров, заданных нами для замены, не обнаружен в исходном тексте программы.
Неподдельно увлеченные гипотетическими проектными расчетами для мнимой технологической машины, авторы натолкнулись на одно из ограничений средства $REPLACE, о котором было сказано выше - для замены доступны те и только те списки параметров, которые явно присутствуют в тексте описания глобального фрагмента. Однако, уже описанными в этом документе средствами в этом задании невозможно добиться такого присутствия списков параметров, разве что распотрошить фрагменты и соорудить единый текст описания структуры машины. В PRADIS имеется, однако, возможность замещать списки параметров и во фрагментах, включенных во фрагмент более высокого уровня. Для этого используется полный формат описания фрагмента. Воспользуемся здесь этим приемом. В раздел описания данных глобального фрагмента включим те списки параметров, которые нам захотелось иметь в разделе REPLACE (F коромысла, F шатуна, масштабы пересчета и т.д.). При этом попутно вспомним, что список параметров "Средний диаметр дисков трения" не используется в описании структуры фрагмента ПРИВОД, а входит в составной список параметров "Параметры муфты". Поэтому для формирования этого списка параметров необходимо в глобальном блоке данных иметь также описание всех параметров, входящих в список параметров муфты. Включение фрагментов привода и исполнительного механизма в подразделе STRUCTURE глобального фрагмента будет в этом случае выглядеть так:
Привод 'ПРИВОД (2 1;
Параметры муфты = Параметры муфты)
Исполнительный механизм'МЕХАНИЗМ (2 1 3;
Масштаб пересчета напр.шатуна =
Масштаб пересчета напр.шатуна,
Масштаб пересчета напр.кором.=
Масштаб пересчета напр.кором.,
F коромысла = F коромысла,
F шатуна = F шатуна)
Привод 'ПРИВОД (2 1;
Параметры муфты = Параметры муфты)
Исполнительный механизм'МЕХАНИЗМ (2 1 3;
Масштаб пересчета напр.шатуна =
Масштаб пересчета напр.шатуна,
Масштаб пересчета напр.кором.=
Масштаб пересчета напр.кором.,
F коромысла = F коромысла,
F шатуна = F шатуна)
После списка узлов подключения каждого из фрагментов задается описание тех списков параметров ВКЛЮЧАЕМОГО фрагмента, которые должны замещаться списками параметров ТЕКУЩЕГО фрагмента.
Конечно, в данном случае придется повторить формирование модели со вновь полученным текстом программы. Зато в дальнейшем можно для замещающих списков параметров пользоваться возможностью $REPLACE.
Внесем исправления в текст программы TEST63 и выполним задание на анализ и формирование модели машины (SLANG TEST63). Разделы описания данных и замены параметров будут выглядеть уже не так оптимистично, как вначале:
$ DATA :
{ Муфта }
Жесткость возвратных пружин = 1. E4
Осевая жесткость полумуфт = 9. E5
Сдвиговая жесткость полумуфт = 1. E9
Рабочий ход нажимного элемента = 0.005
Средний диаметр дисков трения = 0.640
Коэффициент трения = 0.2
Момент инерции первой полумуфты = 1.25
Момент инерции второй полумуфты = 0.10
Масса нажимного элемента = 1
$ REPLACE :
Масштаб пересчета напр.шатуна = 4.E4
Масштаб пересчета напр.кором. = 4.E4
F коромысла = 0.25 E-4 ; F шатуна = 0.25 E-4
Параметры муфты = Жесткость возвратных пружин,
Осевая жесткость полумуфт,
Сдвиговая жесткость полумуфт,
Рабочий ход нажимного элемента,
Средний диаметр дисков трения,
Коэффициент трения,
Момент инерции первой полумуфты,
Момент инерции второй полумуфты,
Масса нажимного элемента;
Результаты расчета нового варианта с усиленной муфтой и ослабленными рычагами привели к таким результатам:
1) Муфта работает лучше, но смыкается все равно поздно. В ходе дальнейшей работы она проскальзывает. Увеличим средний диаметр фрикционных накладок до 1250 мм (максимальный момент на муфте 62н*м, 62/500/0.2/ *2 = 1240).
2) Напряжения в шатуне и коромысле составили соответственно 21.6 МПа и 34 МПа. Есть еще небольшой запас. Уменьшаем площадь поперечного сечения еще в 1.5 раза. Гибкость шатуна составит 66 (коэффициент снижения допускаемых напряжений - 0.38; допускаемые напряжения - 38 МПа). Гибкость коромысла - 33 (соответственно 0.77, 77 МПа).
Новый расчет привел к следующим результатам:
1) Муфта практически не проскальзывает.
2) Напряжения в шатуне и коромысле - 38 и 64 МПа. Это примерно соответствует предельным значениям допускаемых напряжений. Поэтому с "оптимизацией" поперечных сечений профилей завершим.
Однако оглянемся немного назад и посмотрим на дело рук своих. Этакая штучка с рычагами из толстой проволоки приводится в действие приводом, где монументальностью своих размеров выделяется муфта. Ее поперечник приближается к полутора метрам (т.е. Машина - Муфта). Она развивает усилие до 500 Н (!), совершая примерно 1 рабочий ход в секунду. При этом муфта борется в основном не с технологической нагрузкой (пресс ее не замечает), а с инерционностью элементов исполнительного механизма. Аналогов мировое машиностроение не знало и знать не будет. Правда, если шатун действительно имеет такие поперечные размеры, мы, видимо, решили задачку о непересечении рабочей зоны шатуна и стойки (язык не поворачивается сказать, что пресса, скорее - пресс-муфты) достаточно точно.
Наши рассуждения в подразделе 5.3 по поводу некоторых параметров машины, видимо, должны подвергнуться серьезной корректировке, как, видимо, и само "техническое задание" рис.5.1. Во-первых, не очень серьезно городить огород из толстой проволоки. Больше смысла, видимо, несколько увеличить допускаемую нагрузку на ползун (хотя бы до 1000 Н). Например, совместить в одном рабочем ходе ползуна две операции. При этом быстроходность пресса можно уменьшить (двигатель будет восполнять затраченную работу несколько дольше). Уменьшения быстроходности можно добиться за счет увеличения передаточного отношения редуктора в 2 раза. При этом инерционные нагрузки от исполнительного механизма значительно снизятся. Во-вторых, снижение быстроходности машины благотворно скажется на габаритах муфты. Для уменьшения габаритов в реальной конструкции, конечно же, применяются многодисковые фрикционные муфты. Например, усилие прижима фрикционных накладок 500 Н для двухдисковой фрикционной муфты будет эквивалентно усилию 1000 Н для однодисковой.
Итак, внесем в описание машины следующие изменения - передаточное отношение привода - 8, усилие технологической операции - 1000, усилие на нажимном элементе - 1000 (эквивалентное усилие прижима для двухдисковой муфты). Ожидаемое уменьшение габаритов муфты - примерно в 4 * 2 = 8 раз (если не учитывать возросшее влияние технологической нагрузки). Поэтому муфту в первом расчете для нового варианта вернем к первоначальным размерам. Площади поперечных сечений шатуна и коромысла зададим по 0.25 кв. сантиметра. Изменение передаточного отношения привода требует вмешательства в текст фрагмента ПРИВОД, поэтому для выполнения этого цикла изменений требуется сформировать новую модель машины.
После нескольких итераций, оставив поперечное сечение стержней в покое, подобрали средний диаметр фрикционных дисков сцепления муфты. Если этот размер около 300 мм, муфта не проскальзывает.
Для последующих расчетов фрикционных дисков на долговечность можно использовать потери в муфте при включении и проскальзывании. Чтобы получить величину этой энергии, нужно смоделировать выключение муфты в конце рабочего хода пресса. При этом накопленная величина энергии как раз и будет характеризовать работу, затраченную на разрушение фрикционных дисков. Кроме этого, задавая расчет соответствующих выходных переменных, можно решать такие задачи, например, как ориентировочное определение к.п.д. машины, расчеты на долговечность по прочности и износу и т.д.
Нам кажется, что гипотетический проектный расчет на этом нужно закончить, поскольку без учета конкретных условий производства, требований к конструкции и габаритам машины, конструктивной проработки узлов он теряет особый смысл. По нашему мнению, приведенный здесь пример в какой-то степени демонстрирует технологию применения моделирования при проектировании, начиная с эскизных прикидок. Естественно, что от стадии к стадии проектирования, когда проектируемый объект начнет обрастать говядиной, модель будет усложняться. Не исключено, что на каком-то этапе расчет полной модели для вашей ЭВМ станет непосильной задачей, и вам придется применить больше фантазии и изобретательности, формируя гипертрофированные модели, как это делают большие художники. При этом интересующий вас узел прописывается во всю силу вашего мастерства и таланта, а то, что в данном случае лежит вне вашего поля зрения - лишь эскизно, только для создания "рабочей атмосферы" для проектируемого узла. Естественно, что моделирование при этом становится достаточно сложной разновидностью искусства, сплавом опыта и мастерства. Только солидный опыт применения расчетов для реальных практических задач сможет дать вам уверенность в правильности выбора той или иной модели для каждого конкретного рассчитываемого случая. Помни! Что заложил в ЭВМ, то от нее и получишь!
6.4. РЕЗЮМЕ
1. Расчеты принесут больше эстетического удовлетворения, если вы будете пользоваться расширенными возможностями описания изображения объекта (SHOW). При этом можно управлять составом изображения, включая в него те или иные элементы объекта, цветом изображения этих элементов, выбирать для некоторых изображаемых элементов нестандартные графические образы.
2. Основной принцип, положенный в основу формирования изображения: изображение объекта строится из изображений элементов, включенных в описание структуры объекта. С этими, и только этими элементами можно связать какие-либо графические образы. Графические образы объединяются в слои изображения, а из тех, в свою очередь, - формируется одно или несколько изображений объекта, интересующих пользователя.
3. По желанию пользователя, он может связать один или несколько слоев изображения с подвижной системой координат.
4. Контроль локальной точности решения в комплексе PRADIS, как правило, производится по скоростям. Для управления точностью решения используются ключевые параметры программы интегрирования: DRLTX - допускаемая относительная локальная погрешность в районе больших абсолютных значений скоростей ([e]), и DABSX - допускаемая абсолютная локальная погрешность в районе малых абсолютных значений скоростей ([D]). Допускаемая локальная погрешность шага интегрирования для каждой степени свободы определяется по зависимости:
[D] = [D] + [e] * Vc
5. Накопленная погрешность интегрирования может быть как больше, так и меньше суммы локальных погрешностей всех шагов интегрирования. Это определяется характером поведения интегральных кривых в окрестности полученного на данном шаге решения. Если интегральные кривые расходятся (т.е., знаки первой и второй производной совпадают), то накопленная локальная погрешность больше суммы локальных погрешностей всех шагов интегрирования. По этой причине достаточно сложно получить точное значение скорости в районе резких экстремумов интегральных кривых.
6. Применение моделирования при проектном расчете сводится, как правило, к проведению серии последовательных уточняющих расчетов. При этом моделируется какая-либо рабочая для проектируемого объекта ситуация. По результатам моделирования определяются новые, более рациональные значения параметров. Это изменение параметров в общем случае влечет за собой изменение характеристик процессов, поэтому требуется уточняющий расчет. В нашем примере для подбора параметров муфты и стержней потребовалось провести два-три уточняющих расчета.
7. Уголок чистописания. Наша традиционная рубрика содержит две рекомендации, относящиеся к разделу замены параметров (REPLACE).
а) Сохраняйте славную историю замены параметров в каждой конкретной модели. Это можно делать как в комментариях, в исходном тексте программы, так и в документе, специальным образом подготовленном и содержащемся в том же каталоге, что и модель. Не полагайтесь в этом случае на файлы типа T6M или TTT – задания, использующиеся для замены параметров в уже сформированной модели, а, тем более, на свою феноменальную память.
б) Старайтесь формировать модель объекта таким образом, чтобы не обрезать себе в дальнейшем широкие возможности по замене параметров в уже сформированной модели. Для этого рекомендуется заранее предусматривать, какие списки параметров могут быть изменены в дальнейшем, особенно если эти списки параметров входят в блоки данных фрагментов, включаемых в текущий фрагмент. В этом случае используется полный формат описания включаемого фрагмента с указанием доступных для замены списков параметров.
7. ВОПРОСЫ К УЧЕБНОМУ ПОСОБИЮ
ПРИМЕЧАНИЕ. Звездочкой отмечены вопросы повышенной сложности.
7.1. ВОПРОСЫ К ГЛАВЕ 1
1. Назначение комплекса PRADIS.
2. Назовите математические методы, используемые PRADIS для формирования и анализа математической модели объекта.
3. Опишите узловой метод формирования математической модели.
4. Какие уравнения называются топологическими? Какие уравнения приняты в качестве топологических в узловом методе?
5. Какие уравнения называются компонентными? Приведите примеры компонентных уравнений. В каком виде записываются компонентные уравнения для узлового метода?
6. Что представляет из себя математическая модель системы, сформированная по узловому методу? Объясните разницу между способами соединения стержней рис. 1.1.б. и 1.1.в. (*) Что произойдет, если два стержня будут иметь только одну общую степень свободы (например, в направлении оси X). (*) Что будет, если стержни соединены как в примере рис. 1.1б., однако координаты концов обоих стержней разные (в том числе и концов, имеющих одинаковые степени свободы)? Приведите примеры и нарисуйте возможные положения стержней в ходе движения.
7. Перечислите основные методы, используемые вычислительным алгоритмом комплекса PRADIS для получения решения системы ДУ. Покажите связь этих методов друг с другом.
8. Какая информация об объекте и в каком виде представляет собой исходные данные для комплекса PRADIS? Каким образом в программу вводится система ДУ?
9. Опишите рекомендуемый авторами порядок изучения учебного пособия.
7.2. ВОПРОСЫ К ГЛАВЕ 2
1. Назовите процедуры пользователя комплекса PRADIS.
2. Каковы функции процедуры выполнения задания?
3. Поясните понятия "процесс формирования модели" и "выполнение задания для уже сформированной модели".
4. Назовите основные функции процедуры обслуживания системного каталога. Перечислите файлы, появляющиеся в текущем каталоге после процедуры обслуживания системного каталога.
7.3. ВОПРОСЫ К ГЛАВЕ 3
1. Опишите последовательность шагов, которые должен предпринять пользователь для формирования математической модели объекта.
2. Какие другие модели элементов (кроме модели постоянного силового воздействия F) можно было бы использовать для моделирования силы тяжести. Опишите преимущества и недостатки каждого из этих способов Какие другие явления реального процесса можно было бы учесть при использовании каждой из этих моделей?
3. В чем разница процессов колебаний в механических системах рис. 3.1. в случае линейной и нелинейной жесткостей пружин (жесткость нелинейной пружины такова, что в положении статического равновесия она имеет такую же деформацию, что и пружина с линейной жесткостью). Сравните амплитуду и период колебаний в том и другом случае. Как лучше провести это сравнение?
4. Проанализируйте поведение системы рис. 3.1. на достаточно длительном интервале времени. Соответствуют ли получаемые результаты расчета сформированной вами модели объекта? Поведению какого объекта соответствуют получаемые вами результаты?
5. Какова точная величина периода колебаний этого маятника (по формуле из курса физики)? Какой период колебаний маятника получается в результате расчета? Различаются ли периоды 1-го и 5-го колебания? Сможете ли вы объяснить полученные результаты?
6. Перечислите модели элементов, которые стали вам известны в результате изучения материала раздела 3 и в ходе ответов на вопросы.
7.4. ВОПРОСЫ К ГЛАВЕ 4
1. Что такое "программа расчета выходных переменных"? Опишите функции программ расчета выходных переменных в комплексе PRADIS. Какие разновидности программ расчета выходных переменных вам известны?
2. Что такое "внутренние переменные" , "выходные переменные" и "отображаемые переменные"?
3. Что такое "указатель на внутреннюю переменную"? Какие указатели на внутренние переменные используются в комплексе PRADIS?
4. Перечислите программы отображения комплекса PRADIS. Для чего используется каждая из названных вами программ? Опишите известные вам ключевые параметры каждой из программ отображения. Объясните их назначение.
5. Какими способами можно отобразить значение многокомпонентной выходной переменной?
6. Можно ли вторично отобразить результаты расчета без его повторения? Как это делается?
7. Для некоторых программ отображения можно установить верхнюю и нижнюю границы отображаемой переменной. Для каких программ отображения это возможно? Что происходит, если эти границы не установлены? Как по внешнему виду графиков можно узнать, устанавливал ли пользователь границы отображаемых переменных или они были установлены автоматически?
7.5. ВОПРОСЫ К ГЛАВЕ 5
1. Можно ли продолжить прерванный расчет с того места, на котором он был закончен? Опишите, как это делается.
2. Каким образом можно изменить тот или иной список параметров сформированной модели не выполняя ее повторного формирования?
3. Что происходит при совместном использовании разделов $REPLACE и $RESTORE? До или после раздела FRAGMENT должен находиться раздел $REPLACE? А раздел $ RESTORE?
4. Какие ключевые параметры программы интегрирования вам известны? Объясните их назначение.
5. Каким образом рекомендуется получать математические модели сложных объектов? Приведите несколько примеров. Опишите последовательность разделов описания данных и описания объекта в каждом из приведенных вами примеров. Особое внимание уделите понятиям "закрепленный узел" и "внешний узел".
6. Каким образом можно получить изображение объекта?
7. Каким образом изображение объекта помещается в той или иной области экрана и масштабируется? Расскажите о параметрах программы LAYER и их назначении.
8. Какие модели элементов и программы расчета выходных переменных вы знаете? Перечислите степени свободы и параметры названных вами моделей элементов. Назовите порядок следования степеней свободы и параметров.
9(*). Как будет двигаться стержень, описанный следующим образом:
Стержень 'STRGN (1 1 2 2; Точка A, Точка B, Материал)
Опишите поведение стержня при различных значениях списков параметров "Точка A" и "Точка B". Опишите поведение стержня в случае, если одна из степеней свободы (1 или 2) закреплена.
11(*). В разделе описания данных заданы следующие списки параметров:
A = 1, 2, 3
B = 4, 5, 6
Точка A = ...
Точка B = ...
В раздел описания структуры объекта включена модель балочного элемента:
Маятник 'BALKA (A B; Точка A, Точка B, ...)
Предположим, что выполнено задание на формирование модели объекта. Можно ли теперь в разделе $ REPLACE: осуществить такую замену списков параметров:
$ REPLACE:
A = 4, 5, 6
Ответ обоснуйте.
12(*). Как будет работать модель идеально упругого элемента K в случае следующего описания:
Опора 'K (1 2 3 4; Жесткость)
Варианты ответов:
1. Как две независимые пружины одинаковой жесткости. Первая - между степенями свободы 1-3, вторая - между 2 и 4.
2. Как две независимые пружины одинаковой жесткости. Первая - между степенями свободы 1-2, вторая - между 3 и 4.
3. Как одна пружина между степенями свободы 1,2 и 3,4, совершающая плоское движение. Если выбран этот вариант ответа, то поясните, как в этом случае учитываются начальные положения концов стержня.
4. Ваш вариант ответа.
7.6. ВОПРОСЫ К ГЛАВЕ 6
1. Опишите все известные вам возможности раздела формирования изображения объекта $ SHOW.
2. Можно ли в изображение объекта несколько раз включать изображение одного и того же элемента?
3. Какие разновидности программ реализации графических образов вы можете назвать?
4. Поясните понятие "локальная погрешность". С помощью каких ключевых параметров вы можете управлять локальной погрешностью?
5. Можно ли добиться лучших результатов в примере рис.3.1., чем они были получены при ответе на 5 вопрос к 3 главе.